В принципе решение не меняется. Изложенный метод решения задачи отличается тем, что он одинаково пригоден к различхшм системам, описываемым уравнениями любого порядка, и не связан с построением годографов на комплексной плоскости.

§ 20.3. Система с нелинейным корректирующим устройством

На примере конкретной следящей системы (рис. 20.17) рассмотрим некоторые особенности введения специальных нелинейных корректирующих устройств, использование которых приводит к тому, что переходный процесс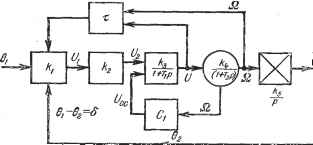

Рис. 20.17.

в системе имеет такой вид, как будто инерционность двигателя во время переходного процесса существенно уменьшается [134].

На рис. 20.18 тонкой линией показано, что при синусоидальных колебаниях вследствие инерционности двигателя ошибка реальной схтетемы бр отстает от ошибки при идеальном двигателе бц на угол ф = arctg ©Г, где со - частота колебаний, Т - постоянная времени двигателя.

Введение нелинейных динамических корректирующих сигналов в данном случае производится таким образом, чтобы деформировать вид кривой ошибки бр, как показано штриховкой на рис. 20.18.

Для отыскания численных соотношений, определяющих зависимость между интервалом введения динамического корректирующего сигнала и эквивалентными параметрами двигателя, разложим заштрихованную кривую (рис. 20,18) в ряд Фурье и сравним с кривой ошибки б при безынерционном двигателе. Ограничиваясь основной гармоникой колебаний, получим

(20.52)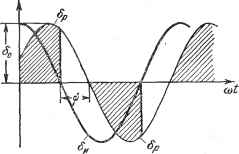

Рис. 20.18.

б = б sin coi -\- 62 cos (iit.

бо I sin (©i-я))) sin чЛ d(ot, 11

62 =

бо j sin {at ~ я))) cos at dat Ф

Заметим, что амплитуда ошибки бц связана с амплитудой управляющего напряжения а соотношением бц == cos ф. При этом выражения для

коэффициентов гармонической линеаризации примут вид

g = [cos ф (я - ф) + sin ф],

=-( -ф).

(20.54)

Поэтому гармонически линеаризованное уравнение двигателя с указанной нелинейной коррекцией будет

/ \ I ? (.0-1 w)

(20.55)

где О.-щ.и обозначенЪх на рис. 20.17.

Оно позволяет совместно с уравнениями остальных звеньев системы проводить анализ системы. Однако использование уравнения (20.55) технически не всегда бывает удобно. Недостатком формы записи его является то, что двигатель, по существу, является инерционньш звеном, в то время как уравнение его получилось в форме уравнения звена с введением производной, причем д < 0.

Для получения передаточной функции двигателя обычного вида необходимо сделать некоторые специальные преобразования. Будем искать ее в виде

с неизвестными пока к* и Г*. Потребуем, чтобы (20.56) и (20.55) были эквивалентны друг другу.

Уравнение (20.56) запишем в виде

(20.57)

и подставим в него значения -т- и Ql из (20.55):

q{a, со)

dV . д (а, (О) dU

+ q{a,a)U+-k*U. (20.58)

Для случая исследования автоколебаний и устойчивости системы выражение для напряжения U принимается в виде

и - а sin &t.

Подставив это в уравнение (20.58) и выделив члены с синусами и косинусами, получим систему уравнений

T*q {а, (д) (д + q {а, со) = О, - T*q (а, а) & + q {а, ©) - /с* = О,

откуда находим

-д>.со) J,*qa)+ ti * . (20.59)

cog (а, со) ч \ / t g со)

Таким образом, передаточная функция двигателя с нелинейной коррекцией имеет вид

т (а, (О)

qa,a)~q{a,a) + -Mp]U. (20.61)

Передаточную функцию двигателя с нелинейной коррекцией, как и прежде, ищем в виде (20.56) или

T*~ + Q = k*U. Подставим сюда значения и Й из (20.61). Получим

q (а. О)) -I q {а, со)] рС7+ +

q{a, со)---g(a, со)] U+-pU=k*U. (20.62)

Затем, учитывая форму решения (20.7), (20.8), запишем выражения

pU = а ( sin ф -Ь со cos я))), pU = а ( - со) sin \р + 2асо cos ф

и подставим их в (20.62). Разделяя там члены с синусами и косинусами, получим систему уравнений

Г* [tog (а, со) -f tq (а, со)] + q (а, со) = О,

Т* Щ {а, со) - tog (а, со)] -Ь g {а, &) - к* = 0.

Отсюда находим выражения для эквивалентного коэффициента усиления и постоянной времени:

[д (а, (й)]2-- g (а, со) д {а, со) к* = q (а, СО) -f-<-, (20.63)

д(а, т)+-д(а, со)

п* - gK to)

д{а, (u)4.-i-g(o, со)

(20.64)

Они отличаются от выражений (20.59), выведенных для случая исследования автоколебаний и устойчивости, наличием членов с tja, характеризующих переходный процесс.

Поскольку в полученные формулы величина показателя затухания входит только в составе дроби g/co, причем практически при исследовании колебательных переходных процессов часто со ] , то во многих случаях и для переходных процессов можно использовать более простые формулы (20.59).

Используя выражения, полученные для коэффициентов гармонической линеаризации (20.54), и выражения для эквивалентных параметров двигателя (20.63) и (20.64), MOHfflo найти общее выражение для эквивалентной постоянной времени двигателя при использовании данного вида нелинейных корректирующих сигналов:

Заметим, что в данном случае д (а) < О и эквивалентная постоянная времени звена Г*, как это и должно быть, положительна.

Из выражения (20.59) видно, что для уменьшения постоянной времени двигателя нужно уменьшить величину \ q (.

Найдем передаточную функцию двигателя с указанной нелинейной коррекцией для исследования переходного процесса.

Вместо (20.55) получим