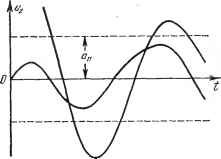Рис. 20.10.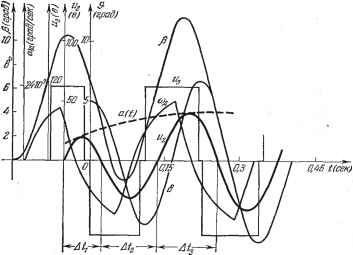

Рис. 20.11.

Пример 2. В главе 17 было рассмотрено точное исследование переходного процесса в идеальной системе с логическим устройством. Исследуем теперь приближенным методом переходный процесс в реальной системе с учетом нескольких постоянных времени, имея в виду, что он сходится к автоколебаниям с некоторой амплитудой а = а , которые изучались в § 18.4.

Найдем зависимости показателя затухания t, и частоты о) от меняющейся в переходном процессе амплитуды а, т. е. зависимости t ( ), ( ) Тогда, зная начальную амплитуду и конечную а = а, можно судить о качестве переходного процесса по соответствующим значениям показателя затухания и частоты ©.

рова [98] при значении параметра = 5 е/град и при начальном значении амплитуды колебаний uq = 250 е. На том же рис. 20.9 изображена пунктиром огибающая переходного процесса, построенная приближенно на основании диаграммы качества (рис. 20.7). Из выполненного построения видно, что

приближенный расчет по методу гармонической линеаризации дает неболь-пгую погрепшость при определении огибающей. На рис. 20.10 показан характер переходных процессов в той же системе при повышенной крутизне датчика рассогласования: к = 10 е/град. В данном случае в установившемся режиме имеют место автоколебания с амплитудой а = 42 е.

На рис. 20.11 построен переходный процесс в той же системе при к = = 10 в/град для случая, когда система приходит к указанному ре?киму автоколебаний от малых начальных отклонений ( снизу ). Там же показана огибающая а (t), найденная по методу гармонической линеаризации на основании диаграммы качества.

Приближенный метод дает достаточно хорошие результаты и в том случае, когда колебания затухают практически за один период (рис. 20.12).

Формула для гармонической линеаризации нелинейности вместо (18.153) принимает вид

Ф{и, v)==lg + {p~Q

где q Ti q определяются прежними формулами (18.154), так как последовательность переключений, согласно рис. 20.13, остается прежней. Но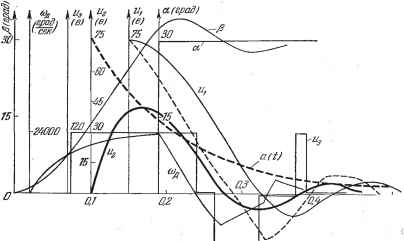

Рис. 20.12.

значения входящих ъ qnq тригонометрических функций (18.151) и (18.152) изменятся следующим образом. При определении Оц и о через а нужно в соответствующие передаточные функции подставить р= С + 7<в, что дает

)2 + 1

(аналогичные выра?кения получаются для и y). Сравнивая их с (18.149), приходим к выводу, что в формулах (18.151) и (18.152) вместо а, Tj©, асо, Tfi) ДОЛЖНЫ быть поставлены соответственно выражения:

-t-t-

-I/,

иЩ \

Рис, 20.13.

(20.50)

В результате q ш q будут функциями всех трех величин: q{a, со, Q; q {а, со, р. Характеристическое уравнение вместо (18.155) примет вид

ЪоР + hp + b,p + Р + к {p~t) + kq {a, CO, 0 = 0,.

bo = ToTgT, by = ToTg + ToT -\- TgT, b To+Tg+ T,

После подстановки р = + по формуле (20.19) получаем вещественную и мнимую части:

Xkq{a,a,l) + bo t+h + bt + t~ (6fco + 3&a S + 2b,) co -b feo®* = 0, Y = kq {a, CO, 9 + {ibo + 3b + 2b2t + i)ti>~ {ib t + 6&i) = 0. Отсюда находим:

kq (a, 0), 0 = /i (o), Q, kq (a, ©, 0 = U ( , D- (20.51)

Будем задаваться разными значениями t, ж & ж строить на основании уравнений (20.51) пинии равных значений и © на плоскости координат к, а

(рис. 20.14). Для этого для заданных , © сначала строится кривая отношения д {a)/q(а) (рис. 20.15). Согласно (20.51) это отношение должно быть равно определенному числу: q (a)/q {а) = == /1 21 leM определится значение а (рис. 20.15) для данных ю. После этого для них вычисляется значение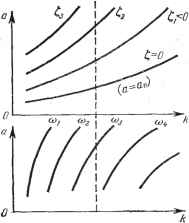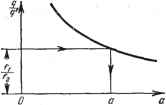

Рис. 20.14.

Рис. 20.15.

к = fi/q. Таким путем по точкам строится вся диаграмма качества нелинейного переходного процесса (рис. 20.14). Линия ? = О соответствует зависимости амплитуды установившихся автоколебаний от коэффициента усиления к.

При любом заданном к изменение показателя затухания t, ж изменение частоты ю во время переходного процесса определится прямой к = const (рис. 20.14, пунктир). Результат показан на рис. 20.16. Это позволяет судить о быстроте затухания и о количестве колебаний за время переходного процесса.

Заметим, что решение задачи несколько упростится при малом t,. В этом случае, считая постоянные времени измерителей Ту и достаточно малыми, можем пренебречь произведениями Tt, ж Tt выражениях (20.50) и пользоваться прежними выражениями q ж q (18.151) с подстановками (18.151) и (18.152). Кроме того, в написан-и У нужно сохранить только первую сте-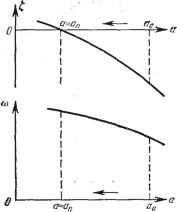

Рис. 20.16.

пых вьппе выражениях для X пень :

X = kqia, &) + t, - (3&it + Sfeg) + &o * = О,

У = kq (а, ©) + {2ЬЛ + 1) © - (4&oS + = 0.