Статическая характеристика нелинейного звена - реле - изображена на рис. 20.6. Выполняя гармоническую линеаризацию нелинейной характеристики реле, получим уравнение

из = q (а) (20.41)

где в соответствии с (18.16) для однозначной релейной характеристики с зоной нечувствительности коэффициент гармонической линеаризации определяется формулой

--l/ (20.42!

Учитывая уравнение датчика рассогласования (20.40), гармонически линеаризованное уравнение реле (20.41) и передаточные функции других линейных звеньев, приведенные на рис. 20.5, запишем уравнение для собственного движения (а = 0) следяш,ей системы в виде

[(JiP -Ы) (ГР + 1) Р + КККЛ (о) Р +

+ kjijcjiq (а)] = 0. (20.43)

Характеристическое уравнение, соответствующее полученному дифференциальному уравнению, будет

(JiP + 1) {Тр -Ь 1) р -Ь kjcjcoq {а)р+ т. 9П

+ kikjijcq (а) = 0. (20.44)

Произведем вначале построение диаграммы качества по первому способу, указанному в § 20.1. Для этого в уравнении (20.44) необходимо произвести подстановку р = -- /© с использованием формулы (20.19).

Вычисляя соответствующие производные характеристического полинома (20.44) по р и подставляя р = t, ъ полученные выражения производных, найдем коэффициенты разложения в ряд уравнения (20.44) при р = t + которое в результате распадается на следующие два уравнения:

X = ТТ, + (Г + Т) -Ь [1 -Ь kjcgkoq (а)] I + kJcsKq ( ) -

- mTt -Ь л -Ь 2 = о, (20.45) Y = mTV +2{Т + Т) t + kkgKq (а)1 to - ГГ© = 0. (20.46) Из последнего уравнения определяем квадрат частоты:

= 7г-[3№22(Г1 + Г2) -bl-bWoc9(a),. (20.47

Подставляя значение в уравнение (20.45), получим TiTt? + {Ti + Га) + [1 + khkooq {а)] t -Ь kikJtgKq (а) =

= -[?>TiT2t-\-2{Ti + T2)l+i + k2hkocq{a)\ [ЗГГаС + + Ta] (20.48)

Построим диаграмму качества для следящей системы по параметру /с, т. е. по передаточному числу (крутизне характеристики) датчика рассогласования. Так как затухание 1, в (20.48) входит нелинейно, то удобно данное уравнение разрешить относительно параметра ку. В результате получим

= W4gH { f + 2 (Г1 + Га) £ +1 + kkgkooq {а)] X

Для построения диаграммы зададимся следующими значениями других параметров: = 0,05 сек, = 0,05 сек, = i, к = 200 град! сек-в, к = 0,01-, /сос = 10 сек-вЬрад, Ъ = Ъ в, с = 120 в.

Подставляя приведенные значения параметров в (20.49) и задаваясь различными постоянными значениями показателя затухания t, - const, строим кривые а (kj) (рис. 20.7). На основании формулы (20.47) при постоянных значениях частоты © = const строим также пунктирные кривые а (kj). Эти кривые представляют собой диаграмму качества для рассматриваемой следящей системы. Кривая а {к) при t = О соответствует автоколебаниям.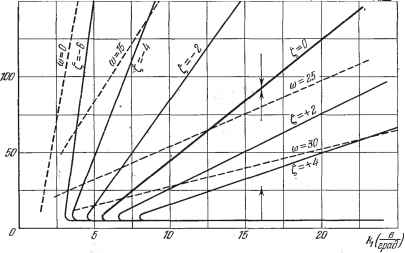

Рис. 20.7.

Выполним теперь построение диаграммы качества по второму способу, указанному в § 20.1.

Уравнение (20.44) запишем в виде

pS+Aip+A2P + As=0,

Ai =

1+МзАос?{ )

Ькфф/д (а)

Формулы (20.32) и (20.33) с этими значениями Ai, А 2, Ag позволяют построить диаграмму затухания нелинейных процессов по любому из параметров системы. Для параметра к при выбранных значениях других параметров следящей системы это дает тот же результат, что и в предыдущем случае.

Аналогичное построение диаграммы качества переходного процесса для той ?ке системы при отключении дополнительной обратной связи дает результат, представленный на рис. 20.8. В данном частном случае линии t, = const и © = const накладываются друг на друга.

Сравнивая полученные диаграммы для случаев наличия дополнительной обратной связи и отсутствия обратной связи, убеждаемся, что за счет обратной связи расширяется область затухающих колебательных процессов (область левее и вьппе линии = О, соответствующей автоколебаниям). Кроме того, при тех же самых значениях параметра к в случае наличия обратной связи в области затухающих процессов получается большее по абсолютной величине затухание, чем без обратной связи. Например, при к = В

Ж а - 90° при наличии обратной связи затухание = -4,.тогда как в случае отключенной обратной связи t, - -2. Это говорит о том, что обратная связь приводит к увеличению быстроты затухания переходного процесса.

Полученные диаграммы качества позволяют оценить переходный процесс в нелинейной системе, если заданы параметры последней, а также дают

а(ерав)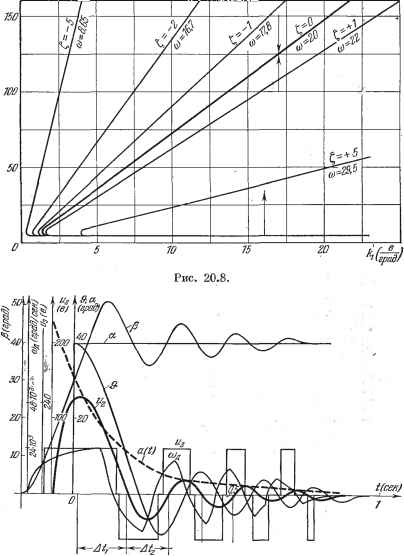

Рис. 20.9.

возможность репшть и обратную задачу, т. е. выбрать значения параметров из условия заданного качества переходного процесса. Кроме того, по диаграммам качества легко построить огибающую амплитуд переходного процесса и найти изменение частоты процесса от периода к периоду, т. е. в конечном счете выполнить приближенное построение переходного процесса.

Для определения погрепшости метода на рис. 20.9 построен переходный процесс в рассматриваемой системе численно-графическим методом Башки-