(20.24)

Итак, если диаграммы качества для разных структурных схем какой- либо автоматической системы построены по различным параметрам (к и др.), то они могут служить хорошим материалом для выбора наилучших параметров нелинейной системы при ее проектировании или синтезе.

Обратимся теперь к способам построения этих диаграмм.

Первый способ. Выделив в уравнении (20.18) вещественную X и мнимую У части, подобно тому как это делалось в главе 18, получим два уравнения:

X (а, со, р = О, У {а, со, О = 0.

Пусть требуется построить диаграмму качества затухания нелинейных колебаний по некоторому параметру системы /с, который входит в коэффициенты уравнений (20.24). Выразив на основании одного из этих уравнений величину

со = Л [а, I, к) (20.25)

и подставив ее в другое из уравнений (20.24), найдем

к = и(а, t). . (20.26)

Тогда, придавая S различные постоянные значения, по (20.26) можно легко построить семейство линий = const на диаграмме качества (рис. 20.2). Затем, используя (20.25), можно построить также семейство линий со = const.

Второй способ. Характеристическое уравнение (20.17) можно записать в развернутом виде:

р + iP - + 2Р - + . . . + An-J> + = О, (20.27)

где все коэффициенты А, А, . . А или часть из них являются функциями искомых величин а, со и g (в простейших задачах только от а). Разложим левую часть уравнения (20.27) на два сомножителя:

(р -2 + Cip - + - - . + С 2) (р + Sip + В), (20.28)

последний из которых соответствует основной паре комплексных корней Pi 2 = ± /со, определяющей колебательный переходный процесс в исследуемой системе. Тогда получаем

, со2 = Б2-е2. (20.29)

Первый из сомножителей (20.28) должен иметь значительно большие по модулю корни, чем второй, чтобы колебательное решение, соответствующее искомым корням pi, 2 при принятых начальных условиях, было основным. Коэффициенты разложения (20.28) связаны следующими соотношениями:

1 = Ci + Bii А = В -\- BCi, , . ., An = Сп-В.

.Для нахождения величин £ и со необходимо, очевидно, в формулах (20.29) выразить коэффициенты В и В через коэффициенты первоначального уравнения (20.27)

В частности, для характеристического уравнения третьей степени + Aip + Ар + Ад = (р + Ci) (р + В + В2) =0

имеем:

1 = Ci + 5i, 2 = 2+ SiCi, Ад = СВ. (20.30)

Чтобы значения и со (20.29) определяли основную часть решения, а третий корень уравнения можно было не учитьшать, нужно, чтобы

Ci AiBi . -

то из (20.29) получаем формулу для квадрата частоты:

- = -£- (20-33)

Формулы (20.22) и (20.23) позволяют строить диаграммы качества для систем третьего порядка.

Аналогично для системы четвертого порядка получаем

+ А + Ар + Азр + А,= {р + Cip + С) {р + Bj> + S2), (20.34) причем

1 = + Si, Л2 - С2 + S2 + CiSi,

3 ~ 12 + 12 А ~ Сф-

(20.35)

Здесь требуется соблюдение того же условия (20.31).

Исходя из выражения предпоследнего определителя Гурвица, аналогичньш путем находим формулу

= ~ 2 (1+20 {[ + (1+20 22-44+18} (

Eni = A3(AiA2~A3)~A\A,

а затем

Третий способ. Рассмотрим часто встречающийся частный случай, когда коэффициенты гармонической линеаризации g и д зависят только от амплитуды а и не зависят от частоты со и показателя затухания что имеет место для нелинейностей вида F (х). В этом случае после подстановки в характеристическое уравнение р = g + /со выражение (20.18) можно представить в виде

где обозначено:

Ин {а) = g (а) + /д (а), + /со) = gg+gj , (20.39)

причем числитель и знаменатель последнего выражения представляют собой, согласно (20.19), многочлены по степеням /со с коэффициентами, зависящими от .

чем определяется верхний предел для значений t, \, которые следует брать при построении диаграммы качества.

Составим предпоследний определитель Гурвица:

= - 3 == (Cl + В) {В + ВС) - Сф = 1 (2 + С1 + CiSi).

Но так как из (20.30) и (20.29) следует, что В + Сф- = АС (Aj, - SJ, Bj = -2t, то полученное выше выражение можно записать в виде

f -71-1 112-431 ц .

2[42+(i+2D] * 2И2 + (1+2ОТ

Далее, поскольку из (20.30) следует, что

Лз Аз

лри =const

Задаваясь различными постоянными значениями \, построим серию кривых (% + /со) как функции от /со при t, = const (рис. 20.4) аналогично тому, как обычно строятся амплитудно-фазовые характеристики линейной

части системы. На том же графике (рис. 20.4)

нанесем линию - г Точки пересечения ее

с линиями {%, -Ь /ю) определяют собой решение уравнения (20.38), а именно для каждого значения t, в этих точках пересечения получаются соответствующие значения

а по кривой- flT) ( кривой VF (g -f -f/co)). Этим самым определяется качество колебательного переходного процесса при всех заданных параметрах системы, т. е. определяются точки одной вертикали на диаграмме качества (рис. 20.2). Повторив такие же построения (рис. 20.4) для различных значений выбираемого параметра системы /с, можно построить и всю диаграмму качества (рис. 20.2).

Способы построения диаграмм, качества для систем второго класса и другие применения диаграмм см. в [100]. Там же рассматриваются несимметричные колебательные процессы и скользящие процессы.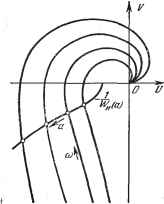

Рис. 20.4.

§ 20.2. Примеры исследования колебательных переходных процессов

Рассмотрим сначала построение диаграммы качества и кривой переходного процесса на примере нелинейной следящей системы, а затем исследуем переходный процесс в нелинейной системе с логическим устройством.

Пример 1. Структурная схема следящей системы изображена на рис. 20.5, где 1 - датчик рассогласования, 2 - усилитель, В - реле.

Рис. 20.5.

Улрав-абъелт

4 - исполнительный двигатель, 5 - редуктор, 6 - управляемый объект, 7 - дополнительная обратная связь.

Системы с такой структурной схемой находят применение в тех случаях, когда для управления двигателем нужна значительная мощность, а увеличение габаритов и веса усилителя нежелательно.

Для датчика рассогласования системы имеем уравнения

щ = /ci (а - Р) = kffy

(20.40)

где аир - соответственно входная и выходная величины системы, к - передаточное число датчика рассогласования, & - рассогласование.