Здесь в общем случае коэффициенты гармонической линеаризации будут зависеть от трех неизвестных: а, со и Если же рассматривается нелиней-иость F (ж), как чаще всего бывает, то g и д сохраняют прежний вид:

2я 2л

д = - j F(as)n ij))sm-ij)dif, gj (asin яр) со8 фйф, (20.14)

и в этом случае можно целиком использовать материал главы 18 в виде готовых выражений g (а) и д (а) для различных конкретных нелинейностей, учитывая, однако, новую форму (20.12) замены нелинейной функции.-

В случае нелинейных систем первого класса дифференциальное уравнение колебательного переходного процесса

Q{p)x + R (р) F {х, рх) = О (20.15)

при наличии свойства фильтра (§ 18.2) после гармонической линеаризации согласно (20.12) принимает вид

Q{p)x + R{p)(q+q)x=0. .(2.16)

Колебательный процесс в линейной системе, описываемый решением (20.1), соответствует паре комплексных корней характеристического уравнения р = g -Ь /со с постоянными значениями и со. Аналогично и колебательный процесс в нелинейной системе, описываемый приближенно формулами (20.7) и (20.8), определяется медленно меняющимися значениями и со, которые можно находить путем определения пары комплексных корней р = + /со характеристического уравнения гармонически линеаризованной системы (20.16).

В соответствии с этим в характеристическое уравнение

Q{p) + R{p)(q+q) = G (20.17)

подставим р = -Ь /со для определения значений и со, удовлетворяющих этому уравнению. В результате получим

<?(e + 7Cu)+i?(e + 7Cu)lg + /g) = U. . (20.18)

Подстановку значения £ -- /со вместо р в любой многочлен удобно выполнять путем разложения его в ряд по степеням /со, например:

+ +(),( . РО.19)

где индекс означает, что в выражения производных надо подставить t, вместо р. По такой же формуле разлагается в ряд и многочлен R {t, -\- /со).

При малых значениях g (для медленно затухающих процессов) вместо (20.19) удобнее применять разложение по степеням t ограничиваясь его первой степенью, а именно:

(C + /co) = (/co)+(-f-) С, ]

Д(е + 7-)=.й(/ ) + ().£, j

где индекс /со означает подстановку /со вместо р в выражения для производных.

В комплексном уравнении (20.18) содержатся три неизвестные: , со и а, причем последняя входит в g и д. Поэтому указанное комплексное уравнение позволяет найти две переменные как функцию третьей:

g = g (а) и со = со (а),

(20.21)

т. е. изменение показателя затухания g и частоты со с изменением амплитуды а затухающего или расходящегося колебательного процесса в нелинейной системе.

Когда функции (20.21) найдены, можно, пользуясь двумя дифференциальными уравнениями первого порядка (20.8), найти а (f) и ф [t) для первого приближения искомого решения нелинейного уравнения (20.15) в форме (20.7). Интегралы уравнения (20.8) имеют при заданных начальных условиях (а = о, ф = фо при i = 0) следующие выражения:

JW = * ф= }со(а)йг + фо,

ао О

(20.22)

где g (а) и со (а) - найденные ранее функции (20.21). Из первого уравнения (20.22) определяется a{t), а из второго-ф (г) после подстановки в него а (t) из первого. В результате получаем решение

X = a{t) sin ф it).

(20.23)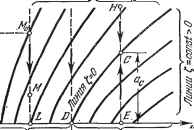

Об/шс/пь ус/поти~ \ DdAacmb автотлебаний еоотп равновЕсц I

Операция, интегрирования (20.22) во многих случаях для оценки качества переходных процессов в автоматических системах не нужна. В большинстве случаев вполне достаточно бывает ограничиться нахождением Линии t=DOH3t<0 функций (20.21) из комплексного

алгебраического уравнения (20.18), так как качество симметричного колебательного переходного процесса вполне может быть охарактеризовано величинами со и их отношением g/co, а также характером их изменения в зависимости от амплитуды колебаний и от параметров системы.

Это достигается построением так называемых диаграмм качества затухания симметричных нелинейных колебаний. Диаграмма на рис. 20.2 представляет собой семейство линий t, = const и линий со = const на плоскости с координатами к, а, причем к означает какой-либо из основных подлежащих выбору параметров системы (коэффициент усиления или др.).

Для линейной системы линии t, = const и со = const в тех же коор- динатах имели бы вид вертикальных прямых, так как показатель затухания и частота колебательных переходных процессов в линейной системе не зависят от величины амплитуды колебаний а, а меняются только с изменением параметров системы (в данном случае К). В нелинейной же системе эти линии искривляются (рис. 20.2) или просто наклоняются в зависимости от формы нелинейности и от общей структуры системы. Это выражает собой изменение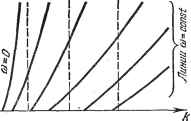

Рис. 20.2.

показателя затухания и частоты со нелинейных колебательных переходных процессов с изменением величины амплитуды колебаний а.

Значение = О соответствует отсутствию затухания, т. е. сохранению с течением времени постоянной амплитуды а. Например, точке С (рис. 20.2) соответствуют колебания с постоянной амплитудой ас (автоколебания). Поэтому линия g = О на диаграмме качества (рис. 20.2) представляет собой не что иное, как зависимость амплитуды автоколебаний от параметра системы к, которая определялась в главе 18. По одну сторону от этой линии лежат линии % = const > О, а по другую - 1, = const < 0. Первые соответствуют расходящимся колебаниям, а вторые - затухающим.

Протеканию переходного процесса во времени соответствует движение изображающей точки М по вертикали (так как амплитуда а в переходном процессе меняется, а коэффициент усиления к сохраняется постоянным), как указано на рис. 20.2 пунктиром и стрелками. Например, значению к в точке L соответствует вертикальная прямая ML. Поскольку эта прямая пересекает линии только с отрицательными значениями , то колебания в переходном процессе будут затухать, т. е. изображающая точка М будет двигаться из некоторого начального положения Мо(где задана начальная амплитуда Яд) вниз. Процесс изменения амплитуды во времени показан на рис. 20.3, а. Изменение частоты со (а) определяется при этом по соответствующей вертикали на нижней части рис. 20.2.

В том случае, когда параметр к в исследуемой системе имеет значение, соответствующее точке Е (рис. 20.2), получается два варианта протекания переходного процесса. Если начальное положение изображающей точки будет ниже точки С {а < ас), то > О, т. е. колебания расходятся и изображающая точка идет, как показано стрелкой на прямой ЕС,

асимптотически приближаясь к точке С. Это соответствует процессу изменения амплитуды колебаний во времени, изображенному на рис. 20.3, б. Если же ао> ас, то g<C О, и изображающая точка пойдет по прямой ЕС вниз (рис. 20.2), что соответствует затухающему переходному процессу (рис. 20.3, в), асимптотически приближающемуся к автоколебаниям с амплитудой ас.

Процессы, аналогичные этому, будут иметь место при любом значении параметра к правее точки В (рис. 20.2). Следовательно, область значений параметра к, лежащая правее точки В, является областью существования автоколебаний, к которой сходятся колебательные переходные процессы с обеих сторон (снизу и сверху). При этом положение равновесия системы (любая точка а = О на оси абсцисс) в данной области значений параметра к является неустойчивым, так как колебания в переходном процессе от него расходятся, стремясь к другому устойчивому состоянию - автоколебательному режиму.

Левее же точки В (рис. 20.2) лежат значения параметра к, при которых переходный процесс затухает от любой начальной амплитуды а до нуля. Это есть область устойчивости равновесного состояния системы.

Левее линии со = О (рис. 20.2) лежит обычно область монотонных переходных процессов.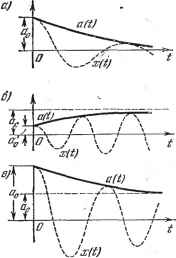

Рис. 20.3.