Нелинейная характеристика типа люфта или зазора. В случае несимметричных колебаний нелинейная характеристика типа люфта или зазора (рис. 19.14) смещается вдоль средней линии, так что ее прежний центр О

переходит в положение О. Постоянная составляющая в этом случае определяется простой формулой

Колебательная составляющая функции 7(ж -1-а8тф) относительно нового центра колебаний не зависит от величины смещения ж . Так, например, шестереночная пара, имеющая люфт, передает движение с тем же передаточным числом для любых углов поворота ведущей шестерни. В случае колебаний в кинематической передаче, включающей данную шестереночную пару, люфт будет проявлять себя одинаково для любых углов поворота. Поэтому для коэффициентов гармонической линеаризации характеристики типа люфта или зазора в случае смещенного центра колебаний относительно начала отсчета будем иметь те же формулы (18.27), что и для случая симметричных колебаний.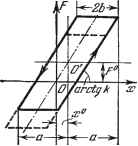

Рис. 19.14.

ГЛАВА 20

ОЦЕНКА КАЧЕСТВА НЕЛИНЕЙНЫХ ПРОЦЕССОВ РЕГУЛИРОВАНИЯ

§ 20.1. Приближенное исследование колебательных переходных процессов

Рассмотрим симметричные относительно оси времени колебательные переходные процессы в нелинейной автоматической системе, которые в первом грубом приближении могут быть описаны затухающей или расходящейся синусоидой с медленно меняющимися во времени показателем затухания и частотой (рис. 20.1).

Прежде чем записать это математически, обратим внимание на два существенных обстоятельства. Для линейных систем, когда показатель затухания t, = const и частота со = const, пишут

X = aoei sin (at + ф). (20.1)

Если же частота ю и показатель затухания t, в процессе колебаний меняются с течением времени, то решение следует записывать в другом виде.

Во-первых, следует писать sin яЬ (t) и определять текущее значение частоты в произвольный момент времени в виде

причем

(20.2)

ф=шйг-Ьфо, (20.3)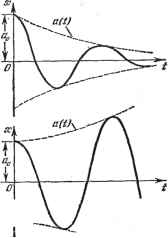

Рис. 20.1.

где 4fio ~ постоянная (начальная фаза). Существует другой способ, когда полагают

я}) = + ф (t) при СОо = const, причем согласно (20.2) текущее значение частоты

- = -?-=-o+. (20.4)

Однако в данной задаче целесообразно придерживаться первого представления ((20.2) и (20.3)).

Во-вторых, при переменном во времени показателе затухания следует определять текущее значение амплитуды а (рис. 20.1) не в виде aeV, как сделано в (20.1), а в виде дифференциальной зависимости

0. J

Тогда в случае линейной системы, когда = const, получаем как частный случай

а в случае нелинейной системы, когда t, меняется в процессе колебаний, текущее значение амплитуды согласно (20.5) будет

= ldt, ааое , (20.6)

т. е. огибающая колебаний (рис. 20.1) состоит из элементарных отрезков экспонент с непрерывно меняющимся показателем t,.

Итак, будем искать решение для переходного процесса в нелинейной системе как первое приближение в виде

ж = asinij), (20.7)

= < - = (20-8)

причем искомыми неизвестными будем считать медленно меняющиеся величины . и со.

Показатель затухания может характеризовать быстроту не только затухания, но и расхождения колебаний:

->о при I: -<о при е<г

т. е. положительным значениям показателя затухания g соответствуют расходящиеся колебания, а отрицательным - затухающие колебания.

Как уже было сказано, величины и со считаются медленно меняющимися функциями. Однако поскольку постоянные значения могут соответствовать в линейных системах как медленному, так и быстрому затуханию колебаний, то и медленно меняющиеся значения могут характеризовать как те, так и другие процессы.

Формулы гармонической линеаризации нелинейности для рассматриваемого случая будут иметь некоторую особенность по сравнению с прежними. В самом деле, если величина показателя затухания t, не мала, то, дифференцируя выражение (20.7) по времени, как произведение двух функций, с учетом (20.8) находим

рх = аа> cos ф -(- sin ф. (20.10)

Отсюда и из (20.7) получаем

sinф = -, cosф = ----IlzLx. (20.11)

Поэтому первая гармоника (затухающая или расходящаяся) нелинейной функции F (х, рх) при X = a{t) sin ф (t) вместо (18.6) здесь будет

F{x, px) = qx+qx(q-jq) х + рх, (20.12)

g = ~ j F (а sin ф, шй cos ф -}-at, sin ф) sin ф йф, о

а = - \ F(a sin ф, oto cos ф-Ь sin ф) cos ф йф.