Вычисляя постоянную составляющую по формуле (19.6), получим

=-ST J + ) = - 2 - Ф1).

После подстановки значений соответствующих углов имеем

2---2п { п -а-- arcsin---j (19.80)

при \ b -- х \ и а I ж - тЬ \.

Далее,

д = - j /(ж-}-(2 8тф)8тя1з£гф=-(со8% -совфг) о

или, сучетом значений углов и xjjg,

при (Z I 6 - ж 1 и й I ж - т6 . Наконец,

2я

q = I (ж + (Z sin я))) cos я)? йя)? = (sin ф- sin я)?!)

или, с учетом соответствующих синусов,

(1-т)

(19.82)

при тех не ограничениях.

Нелинейная характеристика с зоной нечувствительности. Нелинейная характеристика с зоной нечувствительности изобранена на рис. 19.12, а.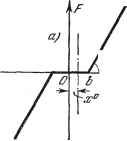

arcsin =arcsin - Рис. 19.12.

Коэффициент q в этом случае равен нулю, так как характеристика однозначная.

Определим значения постоянной составляющей {а, ж ) и коэффициента гармонической линеаризации q (а, ж ) в соответствии с видом функции (ж -]-й sin я)з), показанной на рис. 19.12,6.

Для ПОСТОЯННОЙ составляющей имеем F=~ j /(a;<--ttsini)3)£Zi)3 =

= (cos i)3i - COS + A;a;0 + -- [6 (ф1 - фг) - x° (Ф1 - фг)],

ЧТО после подстановки соответствующих углов дает

Н--6 1 arcsin--arcsin --1 -

-0)0 (

arcsm -

Ъ-хо а

arcsin(19.83)

при (Z Ь + la; !.

Вычисляя коэффщиент q {а, ж ), получаем

q=- j (ж + а sin ф) sin ф йф =

= - 1 A;[asiпф -(Ь -a;0)]sinф£гф-- j /с [а sin ф -(fe-f ж )] sin фсф} =

jt - (ф1 + Фг) -f -- (sin 2ф1 + sin 2фг)

--[(& - ж ) cos Ф1 + (6 + ж ) COS фз],

что с учетом значений углов дает

q~k---arcsm-

Jt \ , а

. Ъ + хО arcsin --

Ь-хО

(b + a:0)2 2

) (19.84)

при а + I х I.

I Нелинейная характеристика с насыщением. Для нелинейной характеристики с насыщением (рис. 19.8) при несимметричных колебаниях аналогичным путем получаем следующие значения постоянной составляющей {а, ж ) и коэффициента гармонической линеаризации q {а, ж ):

F0= А Jt

+ {Ъ -f ж ) arcsin --(6 - ж ) arcsin -

g = - I arcsi при ab -j- \ \.

. b - xO , . b + xO arcsin--h arcsin --

(19.85)

ки .- =

Проиллюстрируем на примере данной нелинейной характеристики графило, /а \ а q л Iа\ = fx (у) ири разных у = const и -f = /а (у) РИ разных у =

= const, вычисленные по формулам (19.85) и представленные на рис. 19.13.

Из графиков для (рис. 19.13, а) видно, что при наличии колебаний входной величины нелинейного звена его статическая характеристика для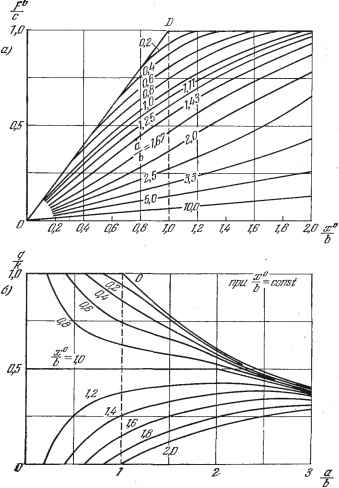

Рис. 19.13.

медленно меняющегося воздействия (функция смещения) сглаживается, причем увеличение амплитуды колебаний входной величины приводит к уменьшению коэффициента усиления нелинейного звена по постоянному или медленно меняющемуся входному воздействию.

Графики для q (рис. 19.13, 6) характеризуют прохождение через нелинейное звено колебательной составляющей в зависимости от амплитуды на входе и смещения центра колебаний. Как видно, увеличение смещения приводит к уменьшению коэффициента усиления для колебательной составляющей.