ности и допустимости таких вибраций в дагшой конкретной автоматической системе. Основными же для качества работы автоматической системы при этом будут являться медленно: меняющиеся процессы, определяемые уравнением (19.68). С точки зрения упрощения их определения весьма вазкными являются следующие два обстоятельства.

Во-первых, вид функции смещения Ф (ж ), как видно из § 19.1, по зависит ни от количества и места приложения внешних воздействий на систему.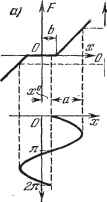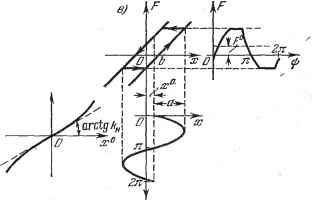

Рис. 19.7.

ни от характера их изменения (если только они медленно меняющиеся). Вид Ф (ж°) зависит от формы нелинейности, от структуры и от параметров системы. Поэтому можно пользоваться любым методом определения Ф (ж ) при любых частных упрощающих предположениях относительно внешних воздействий. Можно, например, пользоваться более простым вторым методом из описанных в § 19.1 методов и проиллюстрировагшых там на примере, взяв любое одно постоянное по величине внешнее воздействие.

Во-вторых, какова бы ни была заданная нелинейность F (ж, рж) (скачкообразная, петлевая и т. п.), обычно функция смещения Ф (ж ) получает вид плавной кривой. Поэтому, в отличие от первоначально заданной нелинейности, ее легко

можно линеаризовать обычным способом (по касательной или по секущей в начале координат или в другом начале отсчета). Имея в виду это свойство, часто вместо термина вибрационное сглаживание употребляют термтш вибрационная линеаризация (будем придерживаться первого из них). Итак, в определенном диапазоне можно считать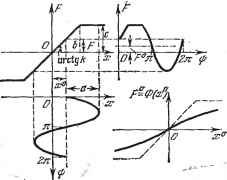

Рис. 19.8.

=Ф (ж ) = кх\

( dxf> )жО=о

(19.70)

Графически представляет собой тангенс угла наклона прямой (касательной или секущей, рис. 19.7, б).

Величина коэффщиента к зависит от соотношения, вообще говоря, всех параметров системы.

Например, для системы, описываемой уравнениями (19.20) - (19.23), согласно (19.53) и (19.50) имеем

Поэтому для расчета медленно протекающих процессов в данной системе на основании (19.20) - (19.22) и (19.70) получаем линейные уравнения:

(Г,р + 1)ж = ад, ж = А()-ж , Л

3-нЖ , ж = 2 Жос, Жос = ьосЖ , \ (19.72)

или единое линейное уравнение (19.24), в котором надо заменить ж на ж и F (ж) на /снж .

Определение коэффициента усиления моншо значительно упростить следующим образом. Поскольку функция смещения Ф (ж°) определяется согласно (19.13) и (19.7) по вырандахию (ж , а, со), в которое подставлена зависимость а (ж ), то формулу для вычисления /Сц меняно представить в виде

, i йФ \ / gFO о йа дРО da, \

н - /жо=о~ \ 8x0 Г да dxO Г- ахо jo

В тех случаях, когда рассматриваются нечетно-симметричные нелинейности F (ж), величтша Z не зависит от со и, кроме того, согласно (19.6)

\ да )хО=0 2п i \ дх /х=авт-ф О

так как производная под знаком интеграла будет четной функцией. Следовательно, для нечетно-симметричных нелинейностей F (ж), как однозначных, так и петлевых, величину ft можно вычислять по формуле

. . к

дхо )хо=о

непосредственно из выранения (19.7), не определяя функции смещения Ф (ж°). Во многих задачах это будет существенным упрощением решения.

Это упрощение не относится к несимметричным нелинейностям, а такне к тем случаям, когда приходится определять не по касательной, а по секущей.

Итак, с подстановкой (19.70) уравнение (19.68) для определения медленно протекающих процессов становится обыкновенным линейным уравнением

lQ{p) + R ip) kj ж = S ip) j it) (19.73)

И, как таковое, легко решается.

Как видим, введенный здесь принцип разделения уравнений для колебательных и для медленно меняющихся составляющих, при котором сохраняются существенно нелинейные свойства системы, приводит к весьма ваянным для практических расчетов результатам. Существенным выводом является то, что медленно меняющиеся сигналы проходят через нелинейность

с другим коэффициентом усиления /Сд, чем автоколебания д или q -\- р)

Особенно важно использовать свойство вибрационного сглаживания нелинейностей с последующей их обычной линеаризацией при расчете слон-ных автоматических систем.

Если, например, система автоматического управления полетом самолета работает по схеме, изображенной на рис. 19.9, то часть системы, обведенную пунктиром (релейный усилитель, привод и дополнительная обратная связь), как отдельную следящую систему, моншо рассчитывать изложенным вьппе методом с учетом автоколебательных вибраций. Частоту последних путем соответствующего выбора параметров этой части системы или введением корректирующих устройств меняно сделать достаточно большой с тем, чтобы амплитуда автоколебаний переменной 2 на выходе этой части системы была

темт/е гиемем/пь/

усшиталь

Привод

Офат/гая связь

1

L !

Рис. 19.9.

мала. Если же указанную амплитуду не удается сделать малой (тогда руль будет колебаться), то необходимо, чтобы указанная частота практически не воспринималась корпусом самолета в процессе его двюкения вокруг центра тянести.

Тогда расчет автоматической системы будет выглядеть следующим образом.

Автоколебания определяем только в обведенной пунктиром внутрешхей части (рис. 19.9), как в отдельной самостоятельной системе, считая х [t) произвольным медленно меняющимся внешнтш входным воздействием, ах - выходной величиной. Для такой простой системы находим, как изложено выше, функцию смещения Ф (ж ), а также частоту и аьшлитуду автоколебаний в зависимости от величины внешнего воздействия. Выбираем параметры данной части системы так, чтобы условия вибрационного сглаживания нелинейности соблюдались во всем практически возможном диапазоне изменения входной величины х. При этом следим за тем, чтобы частота автоколебаний системы (зависящая от параметров системы) лежала за пределами частот возможных колебаний самолета (чтобы она практически не воспринималась корпусом самолета).

После такого расчета внутренней части системы производим обычную линеаризацию функции смещения Ф (ж ), т. е. заменяем ее одной прямой линией = kgX* (причем монно использовать указывавшееся упрощение в определении н). В результате получаем линейное уравнение для медленно протекающих процессов в данной части системы. К этому уравнению добавляем уравнение всей остальной части системы (в данном случае самолета, чувствительных элементов и руля, см. рис. 19.9) и рассчитываем всю систему в целом, как линейную, по любым обычным методам теории автоматического регулирования. При этом не обращаем уне внимания на автоколебания, которые локализуются в рассчитанном ранее внутреннем контуре системы. Однако их влияние не игнорируется, ибо оно было учтено при определении функции смещения Ф (ж ) и коэффщиента кц.