где ж** определяется формулой (19.51) через внешние воздействия. Наконец, из уравнения (19.58) получаем амплитуду автоколебаний переменной ж:

где йц определяется формулой (19.49) через внешнее воздействие, а Шп - формулой (19.48).

Итак, в данной системе имеются все три составляющие ошибки (19.55), зависящие от величины внешних воздействий и от параметров системы. Наиболее нежелательной из них является составляющая ct, возрастающая пропорционально времени. Поэтому систему необходимо видоизменить в первую очередь так, чтобы уничтожить эту составляющую ошибки, т. е. сделать = 0. Для этого можно было бы вовсе изъять дополнительную обратную связь (рис. 19.5), так как при кос = О согласно (19.59) будет = 0. Однако при этом существенно возрастает амплитуда автоколебаний (19.61), т. е. периодическая составляющая ошибки. Поэтому более целесообразной мерой будет замена жесткой обратной связи Жос - 00X4 на гибкую Жос = = косРх. Тогда в уравнении (19.54) величина кос заменится на косР-

{kocTiP + КсР + ki) Ж1 = ж -Ь {Tip + 1) ж* -Ь WS- (19.62)

Как видим, составляющая, пропорциональная времени, в правой части уравнения исчезла, вследствие чего установившееся решение для ошибки ж, в отличие от (19.55), будет

Ж1 = ж -Ь ж*. (19.63)

При этом из (19.62) находим:

? = (а + *о=/Э. (19.64)

причем изменяются, конечно, и формулы для аР, аж (их можно получить таким же способом). Подбором параметров системы амплитуду автоколебаний ошибки можно сделеть весьма малой.

Учитывая (19.25) и (19.27), перепишем данное уравнение в виде (йоеГр + ki+ fcoe) = ж + (Tip + 1) Ж* + кооТП +[koJlt. (19.54)

в соответствии с видом правой части установившееся решение этого линейного уравнения следует искать в виде

xi = 4 + cit + X*, (19.55)

где ж и Ci - постоянные, а ж* - периодическая составляющая.

Подставив это в (19.54), получим три уравнения для отыскания указанных величин:

где 7=, а Юц - частота автоколебаний. Соответственно для астатических систем медленно меняющейся скоростью /(t) будет такая, для которой выполняется условие

\f{t + T)-f{t)\\f{t)\ или </(f).

Указанными свойствами почти всегда обладают полезные сигналы управления, проходящие через автоматическую автоколебательную систему (в том числе в переходных процессах).

Условие медленного изменения любой функции времени монно выразить также и в частотной форме, а именно: медленно меняющейся считается такая функция, возможные частоты изменения которой во времени значительно нине возможной частоты возникающего в системе периодического решения (автоколебаний).

Сделанные предположения позволят величину / (t) или, соответственно, pf (t) считать постоянной за время канедого периода исследуемых автоколебаний и искать решение в той же форме (19.4):

X = аР -\- X*, X* = а sin coi,

где t отсчитывается отдельно внутри каждого периода, ибо теперь ж , а и со будут не постоянными, а переменными во времени t (от периода к периоду) вместе с изменением внешнего воздействия / (i). При этом х (t) будет медленно меняющимся сигналом на входе нелинейности.

В связи со сказанным здесь остается в силе разложение (19.5) - (19.7). Но подстановка его в заданное уравнение нелинейной автоматической системы (19.1) дает

Q (р) (ж + x*) + R (р) (ро + дж* + px-)=S{p)fit).

При достаточно медлешюм изменении функции / (t) (а в астатических системах pf) и величин ж , а, со, входящих в коэффициенты g, g, данное уравнение мояет быть разделено на два отделышх уравнения:

Q (р) х> +Rip)! = S{p)f (t), (19.66)

Q{p)x* + Rip)(q + pjx* = 0, (19.67)

соответственно для медленно меняющейся составляющей и для колебательной составляющей. При этом разделении уравнений, как и прежде, сохраняются существенно нелинейгше свойства системы.

Следовательно, здесь сохраняется целиком прежний (§ 19.1) первый метод решения задачи (второй здесь неприемлем), выраженный формулами (19.10) - (19.13), где в данном случае ж является величиной не постоян-

§ 19.2. Прохождение медленно меняющихся сигналов в автоколебательных системах

Рассмотрим очень важный для практики случай, когда внешнее воздействие / (t), которое может быть либо возмущающим, либо управляющим (задающим), в автоколебательной системе является не постоянным, а медленно меняющимся. Медленно меняющейся будем называть такую функцию времени, которая сравнительно мало изменяется за период автоколебаний, т. е. соблюдается условие в виде одного из неравенств

lf(t + T)~f{t)\<t\f{t)\ или T<t\f{t)\,

НОЙ, а медленно меняющейся. Поэтому прежний процесс решения заканчивается определением функции смещения (19.13). Подставив (19.13) в (19.66), получим дифференциальное уравнение для определения медленно меняющегося сигнала управления ж {() (на фоне автоколебаний системы) в виде

Q{p)x + R{p)Ф (жО) = S{p)f [t). (19.68)

Таким образом, получается, что для определения медленно меняющихся процессов функцию смещения

= Ф (жО) (19.69)

следует подставить в уравнение автоматической системы (19.1) вместо заданной нелинейности F (ж, рх).

Следовательно, функция смещения Ф (ж ) представляет собой как бы статическую характеристику (обычно криволинейн5то), которая определяет зависимость между выходной и входной величинами заданной нелинейности для постоянных или медленно меняющихся сетналов в автоколебательной системе.

При любых нелинейностях, в том числе и скачкообразных, функция смещения Ф (ж ) может получать при определенных условиях вид весьма

плавной кривой. Этот эффект называется вибрационным сглаживанием нелинейностей при помощи автоколебаний, а функцию смещения Ф (ж ) можно называть сглаженной нелинейной характеристикой.

Так, в примере § 19.1 согласно (19.40) функция смещения будет иметь вид рис. 19.6,(2, т. е. для медленно меняющегося сигнала в данной релейной системе нелинейная характеристика будет в определенных пределах иметь плавный вид (рис. 19.6, а) вместо скачкообразного (рис. 19.6, б) - за счет сглаживающего влияния автоколебательных вибраций.

Далее, например, для нелинейностей, обусловленных зоной нечувствительности (рис. 19.7, а), а такне зазором (рис. 19.7, в) и петлей, сигналы X <Ъ при отсутствии автоколебаний не передаются (F = 0). При наличии же автоколебаний сигнал ж -< Ь передается в виде составляющей Р°. Поэтому для медленно меняющегося сигнала получается плавная характеристика (функция смещения) Ф (ж ) без зоны нечувствительности (рис. 19.7, б). Эффект вибрационного сглаживания нелинейностей в этих примерах является положительным (ликвидация зон нечувствительности и петель).

Однако в других случаях эффект вибрационного сглаживания нелинейности может оказаться и отрщательным. Возьмем, например, нелинейную характеристику с зоной насыщения (ограниченно-линейную), показанную на рис. 19.8. В этом случае эа счет того, что верхушки синусоиды с одной стороны срезаются, постоянная составляющая будет меньше, чем само значение F, соответствующее линейному начальному участку. Поэтому постоянный или медленно меняющийся сигнал будет при наличии автоколебаний проходить через данную нелинейность с меньшим коэффициентом усиления, чем без автоколебаний, что может в известных случаях отрицательно сказаться на качестве автоматической системы в целом.

Во многих случаях вычисление а ш & будет необходимо только с точки зрения проверки вьшолнения условий вибрационного сглаживания нелиней-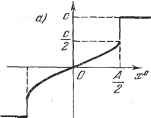

Рис. 19.6.