1) См. конкретные формулы для разных нелинейностей в § 19.3.

Отсюда ВИДНО, что в общем случае все три коэффициента являются функциями трех неизвестных:

а, ш), д а, со), q а, ш). (19.7>

В частных случаях эти зависимости могут быть более простыми ).

Подстановка выражений (19.4) и (19.5) в заданное дифференциальное уравнение (19.1) с учетом свойства фильтра (см. § 18.2) дает

Q {р) (ж +x*) + R (р) ( 7? + дж*+рж* ) = М .

Зто уравнение разбивается на два:

Q (0) + R(0)Fo = М\ (19.8)

Q{p)x* + R(p)[q+p)x-=Q. (19.9).

При таком разделении сохраняются существенно нелинейные свойства и отсутствие суперпозиции решений, так как остается нелинейная взаимосвязь обоих уравнений через соотношения (19.7).

Можно предложить два метода решения задачи.

Первый метод состоит в следующем. Уравнение (19.9) совпадает с прежним уравнением (18.33); отличие состоит лишь в том, что теперь коэффициенты g и д согласно (19.7) зависят не только от а и ш, но и от смещения ж . Поэтому, написав как прежде, характеристическое уравнение

(p) + i?(p)(g+p)=0, (19.10>

заменив р на /ш и выделив вещественную и мнимую части, в отличие ог (18.36), получим здесь два алгебраических уравнения с тремя неизвестными:

X (ж , йп, (Од) = О, У (ж , йп, п) = 0. (19.11)

Эти уравнения дают возможность определить амплитуду Яц и частоту № . автоколебаний как функции постоянной составляющей ж**:

йд (ж ), (о (ж ). (19.12)

Для решения этой задачи можно применять любой из способов, описанных в § 18.2, в зависимости от того, какой из них лучше подходит к условиям-заданной конкретной задачи. Таким же способом можно определить зависимость я и (О не только от ж**, но и от параметров системы с целью выбора последних. Что касается тех способов § 18.2, где используются графики g (я) и д (я), то здесь их необходимо строить в виде серии кривых при разных постоянных значениях ж (рис. 19.3).

После того как из уравнений (19.11) определены зависимости (19.12), можно, воспользовавшись первым из выражений (19.7), найти функцию смещения

F = Ф (ж ). (19.13)

Подставив ее в (19.8), получим алгебраическое уравнение

Q (0) х> + R (0) Ф (жО)=М (19.14)

с одной неизвестной ж , которая отсюда и определяется. Чаще всего это уравнение относительно ж является трансцендентным и решается графически. Затем согласно (19.12) определяются также амплитуда Яд и частота п-

Указанную зависимость (19.12) амплитуды и частоты автоколебаний от величины смещения центра колебаний, характерную именно для нелинейных систем (в линейных системах смещение центра колебаний не играет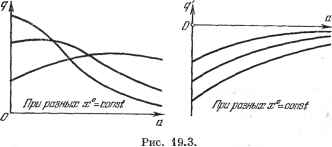

роли), надо всегда иметь в виду. При одних нелинейностях она может быть весьма существенной, при других - менее существенной.

Второй метод решения той же задачи состоит, наоборот, в том, что сначала решается уравнение (19.8), где согласно (19.7) будет (ж , а, о) или часто (ж , а). Решение получает вид

х° (а, со) или хР (а).

(19.45)

Это решение подставляется затем в уравнения (19.11), которые, такш! образом, будут содержать только две неизвестные: и Юд- Определив последние {по любому из способов § 18.2), вычисляем потом по (19.15) и величину зР, которая будет в результате зависеть от формы нелинейности, от параметров системы и от внешнего воздействия ilf .

Величина ж** и является искомой статической или скоростной ошибкой -соответственно для статической и астатической систем.

В тех случаях, когда передаточная функция линейной части системы Л (p)/Q (р) имеет нулевой корень в знаменателе (что часто бывает), т. е. когда Q (0) = О, вместо (19.14) получаем уравнение

. = (19-16)

откуда определяется статическое отклонение или скоростная ошибка х (М*).

В случае, когда при отсутствии внешнего воздействия (ik/* = 0) определяются автоколебания в системе с несимметричной нелинейностью, т. е. нелинейностью F (х) или же F (х, рх), для которой

j F{a sin ф, ceo cos ф) йф = 0] (19.17)

вместо уравнения (19.8) получаем

<? (0) ж -j- /? (0) = 0.

(19.18)

Оно решается любым из тех же двух методов, описанных выше для уравнения (19.8). Одновременно согласно (19.11) определяются ж**, йд, сОд.

Если в этом случае знаменатель Q (р) передаточной функции линейной части системы имеет нулевой корень, то (0) = О и, следовательно, уравнение (19.18) с учетом (19.13) принимает вид

откуда определяется ж**. Это означает, что в указанных системах возникает такое смещение ж** колебаний переменной х, которое ликвидирует свойственную данной нелинейности несимметрию колебаний переменной F (т. е. обеспечивается = 0), как показано, например, на рис. 19.4 в отличие от рис. 19.1, б.

Приведем пример исследования совместного влияния двух внешних, воздействий, причем из дальнейшего будет видно, что, в отличие от линейных

систем, здесь нельзя просто складывать статические ошибки от отдельно взятых воздействий.

Уравнения автоматической системы (рис. 19.5) заданы в виде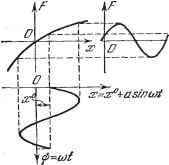

(Г1Р -Ь 1) Ж2 = fcjXi,

1 = fijt) - 4.

(19.20)

Xg - F (ж), ж - Ж2 - Ж{)с, Жод - одЖ,

(19.21)

Рис. 19.4. (2Р + 1) = Ка - и (t),

(19.22)

где F (ж) -[простейшая симметричная релейная характеристика, показанная па рис. 19.15: g

F (ж) = с sign ж. (19.23)

Чтобы воспользоваться выведенными выше общими формулами, надо сначала привести заданную систему уравнений (19.20) - (19.22) к одному

Рис. 19.5.

уравнению типа (19.1). В результате получаем

{Tip + 1) {TV + 1) рх -Ь (Aocip -Ь + fcoc) KF (х) =

= К {тр + 1) Ph (t) + (kooTiP + h + кос) и (t).

(19.24)

Пусть fi (t) является задаюпщм воздействием, изменяющимся с постоянной скоростью:

/х (О = nt, (19.25)

которое требуется воспроизвести на выходе системы в виде х (t). Допустим также, что второе внешнее воздействие /3 (t) является возмущающим и имеет постоянную величину (например, постоянная нагрузка на выходном валу системы):

/2 it) = const = fl. (19.26)

Его влияние требуется свести к минимуму. Найдем установившуюся ошибку на выходе системы. Правая часть уравнения (19.24) будет при этом постоянной, и установившееся решение для ж с учетом автоколебаний следует искать