Примером представления функции времени в виде суммы сопряженных векторов, вращающихся в разные стороны, может служить изображение гармонических функций по формулам Эйлера, например (4.10).

Таким образом, положительные и отрицательные частоты имеют определенный смысл, так как они соответствуют положительным и отрицательным угловым скоростям вращения векторов на комплексной плоскости.

В принципе можно ограничиться рассмотрением только положительных частот. Однако при использовании всего диапазона частот от -оо до -j-oo многие формулы получают более удобный и симметричный вид.

Длина вектора, проведенного из начала координат в точку а. ф. х., соответствующую какой-то выбранной частоте, равна модулю частотной передаточной функции. Угол между вектором и положительным направлением вещественной оси, отсчитываемый против часовой стрелки, равен аргументу или фазе частотной передаточной функции. Таким образом, а. ф, х.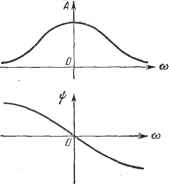

Рис. 4.8.

Рис. 4.9.

.дает возможность наглядно представить для каждой частоты входного воздействия звена отношение амплитуд выходной и входной величин и сдвиг фаз между- ними.

Построение а. ф. х. по вещественной и мнимой частям частотной передаточной функции, как правило, является трудоемкой работой, так как умножение частотной передаточной функции на комплексную величину, сопряженную ее знаменателю, повышает в два раза степень частоты в знаменателе. Обычно гораздо проще строить а. ф. х., используя полярные координаты, т. е. вычисляя непосредственно модуль и фазу. Зная модуль и фазу, можно легко построить соответствующую точку на комплексной плоскости. В случае необходимости при известных модуле и фазе легко вычислить вещественную] и мнимую части умножением модуля на направляющий косинус между вектором и соответствующей осью.

Вместо а. ф. х. можно построить отдельно амплитудную частотную характеристику (а. ч. х.) и фазовую частотную характеристику (ф. ч. х.). Это построение показано на рис. 4.8.

Амплитудная частотная характеристика показывает, как пропускает звено сигнал различной частоты. Оценка пропускания делается по отношению амплитуд выходной и входной величин.

Фазовая частотная характеристика показывает фазовые сдвиги, вносимые звеном на различных частотах.

Как следует из сказанного выше, модуль частотной передаточной функции представляет собой четную функцию частоты, а фаза - нечетную функ-

цию частоты. Поэтому по результатам вычисления модуля и фазы для положительных частот можно сразу построить а. ч. х. и ф. ч. х. для всего диапазона частот -оо <; со < +00.

Можно построить также отдельно вещественную и мнимую частотные характеристики по функциям U (ю) и V (to). Это построение показано на рис. 4.9. Как следует из сказанного выше, вещественная характеристика представляет собой четную функцию частоты, а мнимая характеристика - нечетную функцию частоты.

Минимально-фазовые звенья и системы. В случае, если корни числителя и знаменателя передаточной функции W (р) звена лежат в левой полуплоскости (при этом корни числителя и знаменателя частотной передаточной функции W {]&) лежат в верхней полуплоскости), такое звено называется минимально-фазовым. Как будет показано ниже (см. § 4.8), этим звеньям присущи меньшие по абсолютной величине фазовые сдвиги по сравнению со звеньями, у которых это условие не выполняется.

Можно показать [121], что для минимально-фазовых звеньев существуют следующие зависимости:

+ 00

3t J и -

F(co) =

In cth

(4.17)

где L {и) = \n A (и), % - In, a и - переменная интегрирования.

Приведенные зависимости являются чрезвычайно важными, так как показывают, что частотная передаточная функция минимально-фазового звена или системы полностью определяется заданием ее вещественной части U (со), или мнимой части V (to), или модуля А (ю). Это позволяет упростить задачи анализа и синтеза минимально-фазовых систем, ограничиваясь, например, рассмотрением их вещественных или амплитудных частотных характеристик.

§ 4.4. Логарифмические частотные характеристики

Прологарифмируем выражение частотной передаточной функции (4.16): In W (/(о) = 1пА (ю) 4- /Ф (to). (4.18)

Как видно из зтого выражения, логарифм частотной передаточной функции равен комплексному выражению, вещественной частью которого является логарифм модуля, а мнимой - фаза.

Для практических целей удобнее пользоваться десятичными логарифмами и строить отдельно логарифмическую амплитудную частютную характеристику (л. а. X.) и логарифмическую фазовую частотную характеристику (л. ф. X.). Для построения л. а. х. находится величина

L (to) = 20 Ig I (/to) I = 20 Ig Л (to). (4.19)

Эта величина выражается в децибелах. Бел представляет собой логарифмическую единицу, соответствующую десятикратному увеличению мощности. Один бел соответствует увеличению мощности в 10 раз, 2 бела - в 100 раз, 3 бела - в 1000 раз и т. д.

Децибел равен одной десятой части бела. Если бы А (to) было отношением моп;ностей, то перед логарифмом в правой части (4.19) должен был бы стоять множитель 10. Так как А (со) представляет собой отношение не mohi;-ностей, а выходной и входной величин (перемещений, скоростей, напряжений, токов и т. п.), то увеличение этого отношения в десять раз будет соответствовать увеличению отношения йощностей в сто раз, что соответствует двум белам или двадцати децибелам. Ноэтому в правой части (4.19) стоит множитель 20.

Один децибел соответствует изменению амплитуды в 10 раз, т. е. представляет сравнительно малую величину.

Необходимость логарифмировать модуль частотной передаточной функции (4.19) приводит к тому, что, строго говоря, л. а. х. может быть построена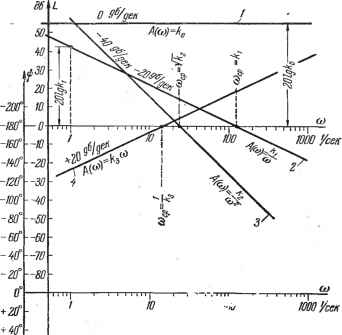

1-I i 1 1И--г-

Рис. 4.10.

только для тех звеньев, у которых передаточная функция представляет собой безразмерную величину. Это возможно при одинаковых размерностях входной и выходной величин звена. В дальнейшем изложении будет подразумеваться именно этот случай.

Однако л. а. х. может условно строиться и для тех звеньев, у которых передаточная функция имеет какую-либо размерность. В этом случае некоторая исходная величина, соответствующая размерности передаточной функции, принимается за единицу (например, 1 г-см1град, 1 сек \ 1 el рад и т. п.) и под значением А (со) понимается отношение модуля частотной передаточной функции к этой исходной единице.

Это же замечание относится и к угловой частоте (о, которая имеет размерность {сек~Ч и которую приходится логарифмировать в соответствии с изложенным.

Для построения л. а. х. и л. ф. х. используется стандартная сетка (рис. 4.10). По оси абсцисс откладывается угловая частота в логарифмиче-