тельно, могут иметь место устойчивость системы в малом (до амплитуд Ящ) и автоколебательный процесс с большой амплитудой, к которому стремится система при начальных амплитудах переходного процесса, превышаюпщх значение йщ-

Заметим, что точку пересечения D кривой W (/ш) с линией -{а) можно найти без построения кривой МлзО*) непосредственно по амплитудно-фазовой характеристике {]&) линейной части системы без элемента запаздывания. Для этого нужно на кривой Wj[ (/ш) найти такую точку Шп (рис. 18.45, г), которая бы при повороте вектора на угол тшп попала на линию -Мд (а), что и даст нам точку D (величина запаздывания т задана, п неизвестна). Условие для определения Шд будет

Топ + I Рл I = я;

после этого находится величина I = А, а затем амплитуда автоколебаний Яда по графику рис. 18.45, д.

В данном параграфе применялись амплитудно-фазовые частотные характеристики. Использование логарифмических частотных характеристик см. в § 20.4.

В заключение заметим, что при исследовании нелинейных автоматических систем применяются еш,е приближенные методы Б. В. Булгакова (см.. [19] или [98]), которые здесь не излагаются.

ГЛАВА 19

МЕДЛЕННО МЕНЯЮЩИЕСЯ ПРОЦЕССЫ В АВТОКОЛЕБАТЕЛЬНЫХ СИСТЕМАХ

§ 19.1. Статические и скоростные ошибки автоколебательных систем

В предыдущих главах исследовались симметричные автоколебания как результат свободного движения системы (т. е. без внешнего воздействия) лри симметричных нелинейностях. Однако, как будет показано, важное практическое значение имеет также рассмотрение несимметричных автоколебаний.

Несимметрия автоколебаний может вызываться различными причинами:

1) несимметричностью нелинейной характеристики как при наличии, так и при отсутствии внешних воздействий;

2) наличием постоянного или медленно меняющегося внешнего воздей-ствия при симметричных нелинейностях;

3) наличием постоянной или медленно меняющейся скорости изменения внешнего воздействия при симметричных нелинейностях (для тех случаев, когда постоянное воздействие не вызывает смещения центра колебаний; обьгано это имеет место в следящих системах и вообще в астатических системах).

В самом деле, если имеется несимметричная нелинейная характеристика (например, рис. 19.1, а, б), то даже при симметричных колебаниях переменной х = а sin <ut возникают несимметричные по амплитуде колебания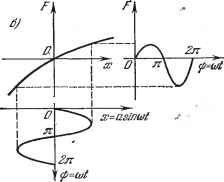

Рис. 19.1.

переменной F (рис. 19.1, б). Если же нелинейность симметрична (например, рис. 19.2, й, б), то при наличии постоянного внешнего воздействия (или ;в астатических системах при наличии постоянной скорости изменения внеш-

него воздействия) смеш,ается центр колебаний переменной ж=ж* + я sin at, шследствие чего колебания переменной F становятся несимметричными по амплитуде и по времени (рис. 19.2, а) или только по времени (рис. 19.2, б).

(p=Ojt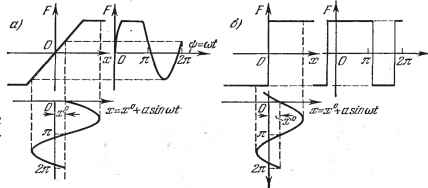

Рис. 19.2.

Пусть задана автоматическая система, динамика которой описывается уравнением

Q{p)x-\-R{p)F (х, рх) = S{p)f (t). . (19.1)

В данном параграфе будем считать f (t) = const = / для статических систем или же pf (t) = const = /J для астатических систем. Астатической системой называется такая, в которой многочлен S (р) имеет общий множитель р, т. е. S (р) = pSi (р).

Поэтому запишем уравнение (19.1) в виде .

Qip) х +Rip) Fix, рх) = М, (19.2)

где соответственно

М° = S (0) f или М° = il (0) . (19.3)

При этом решение нелинейного уравнения (19.1), в отличие от прежнего (§ 18.2), ищется в форме

X = хР -\- X*, где X* = а sin at, (19.4)

причем ж , а, а являются неизвестными постоянными.

С учетом величины смещения х первые члены разложения в ряд Фурье вместо (18.6) и (18.7) следует записать в виде

F ix, рх) = F-\- дж* jpx* -\- высшие гармоники.

(19.5)

тде при обозначении я}) = caf

F° = j F (ж -- а sin ф, асо cos ф) йф, о

q ~ j F ix°-\-a sin ф, асо cos ф) sin ф сг]), о

(ж --Я sin ф, асосо8ф) со8фйф.

(19.6)