тирная кривая). В первом случае получаем точку пересечения D, определяющую периодическое решение (вд, сОп)- Оно будет устойчиво (т. е. соответствует автоколебаниям), так как кривая Ил (/ш) охватывает участок прямой -М{а) с меньшими амплитудами (линейная часть согласно (18.221) нейтральна, вследствие чего этот критерий можно применять). Во втором же случае кривая (/со) пересекается с прямой -(а) только в точке, где а = О, to = оо, т. е. автоколебания отсутствуют (конечная амплитуда получится, если учесть постоянную Га)-

Амплитуда автоколебаний в первом случае определяется по расстоянию I (рис. 18.44, а) на линии -Мн (а) до точки пересечения, причем с учетом (18.222) получаем

(18.223)

где I берется из графика или вычисляется по формуле

I = -С/л (сОп),

причем величина частоты автоколебаний сОд находится из условия

Гл (сОд) = О,

если С/л (сОд) и Fn (сОд) обозначают вещественную и мнимую части выражения Ил (ую) при кос = О, т. е.

Отсюда видно, например, что с увеличением передаточного числа регулятора kjig увеличивается амплитуда автоколебаний.

Для характеристики реле в виде рис. 18.20, а поведение системы без жесткой обратной связи поясняется рис. 18.44, б. Здесь автоколебания могут отсутствовать (кривая 1 рис. 18.44, б), возможно одно периодическое решение (кривые 2 ж 3, пересекающиеся в точке В) или два периодических решения (кривые 2 ж 4, пересекающиеся в точках А ж С). При этом кривая 3 соответствует меньшим, а кривая 4 - большим значениям т в релейной характеристике (см. рис. 18.39). Точки В ж А отвечают устойчивым автоколебаниям. Точка С отвечает неустойчивому периодическому процессу, что может означать устойчивость системы в малом (при а <: ас) и стремление к автоколебательному процессу с амплитудой a = aj в большом. Величины амплитуды и частоты автоко-Рис. 18.44. лебаний определяются по

: самим кривым в точках

i их пересечения.

В данном случае влияние величины передаточного числа кф регулятора без жесткой обратной связи заключается в том, что с увеличением кфд осуществляется переход от кривой 1 к кривой 2 (рис. 18.44, б), т. е. авто-

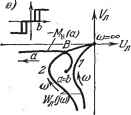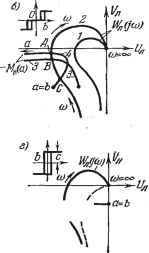колебания в системе появляются только тогда, когда передаточное число кк превзойдет некоторое граничное значение, определяемое моментом касания кривой 1 с кривой S или 4.

Аналогично определяются автоколебания и при наличии жесткой обратной связи, как показано на рис. 18.44, е.

Наконец, при чисто гистерезисной характеристике реле получаем только автоколебательный процесс (рис. 18.44, г), амплитуда и частота которого без жесткой обратной связи определяются точкой Е, а при наличии жесткой обратной связи - точкой Н.

Во всех рассмотренных случаях, как и вообще в рассматриваемом частотном методе, через ад обозначается амплитуда автоколебаний входной величины нелинейного звена, т. е. в данном случае величины х. Чтобы определить амплитуду ае автоколебаний регулируемой величины 6 (температуры), надо найти передаточную функцию, связывающую величины а; и 6:

и следовательно.

kiOn

у (felfe2-l-ftoc)2-l-feScri4 Для системы без обратной связи [кос = 0)

6 =

Аналогично можно определить амплитуду первой гармоники автоколебаний для других переменных в данной системе.

Учет временного запаздывания в реле. В рассматриваемом выше примере системы автоматического регулирования температуры, считалось, что в характеристике реле рис. 18.20 величины Ъ, Ъ, Ъ заданы постоянными, т. е. считалось, что характеристики реле имеют обычный гистерезисный вид

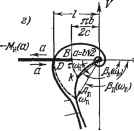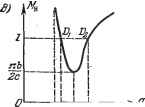Рис. 18.45.

С заданным по входной координате отставанием в срабатывании реле. Теперь же будем считать, что имеются данные запаздывания во времени срабатывания и отпускания реле (одинаковые). Такое нелинейное звено с запаздыванием можно разбить на два элемента: 1) обычное нелинейное звено, характеризующееся графиком рис. 18.45, б или в, и 2) элемент запаздьшания (рис. 18.45, а), описываемый уравнением

Х% = X€ V.

2 \ . (18.226)

-п (Bл<0).J

Рл (COfe) - TfeCOfe = - я (Рл < 0).

Из первого условия определяется величина со, и из второго - критическое время запаздывания:

Ть = -[я-1-рл(соь)] (Рл<0). (18.227)

Такое решение можно найти непосредственно из графика W (/со) или же аналитически, используя выражение (18.220).

Если же реле не имеет зоны нечувствительности, т. е. 6 = О, то точка В попадет в начало координат на рис. 18.45, г и автоколебания будут при любом значении времени запаздывания в срабатывании реле (ть = 0). Поэтому вьподно, чтобы временное запаздывание в реле, рассматриваемое здесь, было бы сравнительно малым, а зона нечувствительности имела бы большую величину (но не превышала допустимых значений, полученных из статического расчета точности регулирования).

Амплитуда и частота автоколебаний при наличии запаздывания определяются следуюп],им образом. Точка пересечения D (рис. 18.45, г) дает два периодических решения, так как в ней на прямой -Мн (а) имеются два значения а. Это следует из графика рис. 18.40, а, причем на основании (18.16) имеем

Mn{a) = -iJ = -J (18.228)

ЧТО изображается графиком рис. 18.45, д. Расстоянию от начала координат I точки пересечения D на рис. 18.45, г соответствуют две точки графика Di и на рис. 18.45, д, которые дают два значепия амплитуды: и ада-Частота сОд обоих периодических решений одинакова и определяется точкой D на кривой (/со).

При этом периодическое решение с меньшей амплитудой будет неустойчивым, а с большей амплитудой Ода - устойчивым, так как в первом случае точка с положительным приращением Аа на линии -Мд (а) охватывается кривой Whs (/со), а во втором случае - не охватывается. Следова-

Тогда можно будет записать выражение амплитудно-фазовой характеристики линейной части системы вместе с элементом запаздывания в виде

Илз (7(0) = Ил (7С0) е--- = e-i . (18.225)

Правило построения такой характеристики описано в главе 14.

Пусть реле (после выделения элемента запаздывания) характеризуется графиком рис. 18.45, б. В этом случае для системы с жесткой обратной связью получим соответственно кривые (/со) и Wa (/ >), изображенные на рис. 18.45, г, а также прямую -М (а) на основании формулы (18.213) и рис. 18.40, а. Если кривые Wg (/со) и -М (а) пересекаются, то будут иметь место автоколебания. Но, как видно из рис. 18.45, г, при достаточно малых запаздываниях т указанные кривые могут не пересекаться, т. е. автоколебаний не будет.

Здесь, как и в линейных системах, можно определить критическое время запаздывания, до которого автоколебания отсутствуют, без построения кривой Плз (/со), а только по кривым Ил (/со) и -Мц{а). В самом деле, в критическом случае некоторая точка кривой Илз (/со) попадет в крайнюю точку В (рис. 18.45, г). Это, как видно из чертежа, соответствует такой точке К кривой (/со), в которой