(рис. 18.41, а и б). В точке пересечения из кривой (/со) берем значение частоты со п, а из кривой - Мн (а) берем величину амплитуды искомого периодического решения. Рис. 18.41, а соответствует системе с нелинейным звеном, имеюн],им гистерезисную петлю, когда согласно (18.210) и (18.213)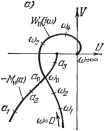

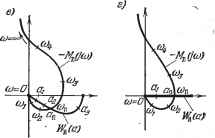Рис. 18.41.

характеристика Мн {а) комплексна. При отсутствии гистерезисной петли, когда Мн (а) веп1;ественна, получаем график рис. 18.41, б. Вместо (18.217) можно пользоваться также выражением

(18.219)

т. е. искать решение как точку пересечения амплитудно-фазовой характеристики нелинейного звена с обратной амплитудно-фазовой характерчстикой линейной части системы, взятой с обратным знаком (рис. 18.41, в ж г).

Устойчивость найденного периодического решения грубо оценивается следующим образом (этот метод не является строго обоснованным, но во многих случаях его применения достаточно). Дадим малое приращение амплитуде: я = йд -Ь Ла. Тогда при положительном Ла получим на кривой - Мн (а).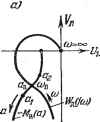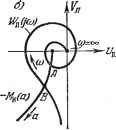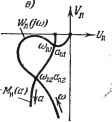

Рис. 18.42.

например, точку (рис. 18.42, а), а при отрицательном Ла - точку а. Для устойчивости периодического решения требуется, очевидно, чтобы при положительном Ла колебания затухали, а при отрицательном Ла - расходились. Для этого согласно частотному критерию (§ 6.5) в случае устойчивой или нейтральной разомкнутой цепи требуется, чтобы суммарная амплитудно-фазовая характеристика W (а, со) в первом случае не охватывала точку (-1, /0), а во втором - охватывала. Но общая характеристика W {а, со) не чертится в рассмотренном способе. Поэтому высказанное положение надо перенести на свойства кривых (/со) и -Мн (а).

Отсюда получаем, что для устойчивости периодического решения (если линейная часть системы в разомкнутом состоянии устойчива или нейтральна) требуется, чтобы амплитудно-фазовая характеристика линейной части Wn (/ш) не охватывала точку а, соответствующую положительному Да, и охватывала точку а, соответствующую отрицательному Да. По этому признаку графики рис. 18.42, а и б (в точке В) дают устойчивое периодическое решение, которое соответствует автоколебаниям замкнутой системы с частотой Шпг и амплитудой ада-

На графике рис. 18.42, е значения сощ и соответствуют неустойчивому, а значения (0п2> jj - устойчивому периодическому решению. Это в простейшем случае может означать устойчивость системы в малом (до амплитуды fini) и автоколебания с частотой сОдг и амплитудой ап2, если начальная амплитуда колебаний в переходном процессе превышает значения а,.

В таких исследованиях предполагается, что все параметры системы заданы в числовом виде (или амплитудно-фазовые характеристики звеньев в виде определенных графиков). Если же требуется выяснить влияние одного или двух каких-нибудь параметров системы, то надо рассмотреть все возможные комбинации кривых W (/со) и -(а) при разных значениях этих параметров.

Рассмотрим примеры.

Система автоматического регулирования температуры. Уравнения системы автоматического регулирования температуры с релейным звеном

Объект и чувствительный элемент

Объект и чувстеите/гьный элемент с включением тной связи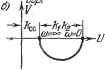

СОгО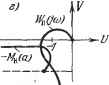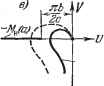

W(Jco)

Рис. 18.43.

были описаны в примере 5 § 18.3. Выражение амплитудно-фазовой характеристики линейной части системы с добавлением жесткой обратной связи будет

Ил (/со)

В данном случае очевидно, что общий знаменатель передаточной функции линейной части системы

Ы = + 1) {Тдр + 1) р (18.221)

не имеет корней с положительной вещественной частью, а нулевой корень говорит о том, что линейная часть системы нейтральна.

Выражение, стоящее в квадратных скобках (18.220), при ко = О (система без обратной связи) соответствует апериодическому звену (регулируемый объект и чувствительный элемент). Оно изображено на рис. 18.43, а. При наличии же жесткой обратной связи в системе (йос ф 0) этот график сдвигается вправо на величину кос (рис. 18.43, б).

Множитель перед квадратной скобкой (18.220) соответствует апериодическому интегрируюн],ему звену (привод с регулируюн],им органом). Он изображен на рис. 18.43, в.

Перемножением этих характеристик получаем амплитудно-фазовую характеристику (/со) линейной части системы (в разомкнутом состоянии) соответственно при отсутствии обратной связи (рис. 18.43, г) и при наличии жесткой обратной связи (рис. 18.43, д). Нанесем на эти же графики кривую обратной по величине и по знаку амплитудно-фазовой характеристики - Мн (а) нелинейного звена (в данном случае - реле). Здесь эта кривая изображена в соответствии с рис. 18.39, б для того случая, когда реле характеризуется графиком рис. 18.20, а, причем = Ъ, bi = тЪ.

Как видно из рис. 18.43, г, в данном случае в замкнутой системе регулирования без обратной связи возможны автоколебания, так как кривые Wn (/со) и -Мн (а) пересекаются, а введением обратной связи можно уничтожить эти автоколебания (рис. 18.43, д). Очевидно также, что и выбором параметров линейной части системы (т. е. деформацией кривой на рис. 18.43, г) можно было бы уничтожить автоколебания замкнутой нелинейной системы и без обратной связи. Напротив, неудачный выбор параметров может привести к автоколебаниям системы даже и при наличии жесткой обратной связи, если на рис. 18.43, д кривые пересекутся. Чем меньше гистерезисная петля (рис. 18.20, а), тем больше будет т (рис. 18.39) и тем легче, как видно из рис. 18.39, б и рис. 18.43, г, д, сделать замкнутую систему устойчивой.

Когда реле имеет чисто гистерезисную характеристику (рнр. 18.20, г), кривая -Мн (а) вырождается согласно рис. 18.39, б (т = -1) в прямую (пунктир на рис. 18.43, д), причем добиться уничтожения авгоколебаний в этом случае нельзя, а можно бороться лишь за уменьшение их амплитуды.

Если в характеристике реле с зоной нечувствительности не будет гистерезисной петли (рис. 18.20, б), то согласно рис. 18.40, а и формуле (18.213) обратная амплитудно-фазовая характеристика нелинейного звена -Мн {а) будет вещественной, как показано на рис. 18.43, е ж ж. При этом замкнутая система без обратной связи может иметь автоколебания, если (/со) примет очертание, показанное пунктиром (рис. 18.43, е). Введение же жесткой обратной связи, как видно из рис. 18.43, ж, полностью уничтожает автоколебания.

Из этого предварительного рассмотрения можно сделать вывод, во-первых о важном стабилизирующем свойстве дополнительной жесткой обратной связи в системе и, во-вторых, о стабилизирующем свойстве зоны нечувствительности реле. С точки зрения устойчивости системы выгодно увеличивать и то и другое. Однако эти возможности ограничены из-за увеличения статической ошибки системы при усилении жесткой обратной связи и при увеличении зоны нечувствительности реле. Последнее связано с тем, что система может находиться в состоянии равновесия в любой точке зоны нечувствительности; получается не одно определенное состояние равновесия, а целая область возможных состояний равновесия с разными значениями регулируемой величины.

После сделанных предварительных заключений перейдем к определению амплитуды и частоты автоколебаний в тех случаях, когда последние имеют место.

В случае идеальной релейной характеристики в соответствии с (18.211) и (18.18) имеем

-Ms{a)=-=-a . (0<а<оо) (18.222)

(Мн (а) заполняет всю отрицательную вещественную ось, рис. 18.44, а). Поэтому Ил (/ >) при отсутствии жесткой обратной связи (сплошная кривая) пересекает ее, а при наличии жесткой обратной связи не пересекает (пунк-