Задаваясь разными значениями амплитуды Oj и вьгаисляя каждый раз по формулам (18.201) - (18.203) значения q (aJ, cOj и к, получим графики flj (к) типа рис. 18.14, но уже для уточненного значения амплитуды первой гармоники периодического решения.

Для заданного значения к == 140 это уточнение дает % = 2,39 е, сй = = 117,8 сек~. Значения эти достаточно близки к величинам первого приближения, а подсчитанная выше амплитуда третьей гармоники достаточно мала.

Пример 2. Пусть в системе автоматического регулирования используется двухфазный индукционный двигатель, описываемый нелинейным уравнением (18.119). В примере 7 § 18.3 найдены автоколебания для первого приближения в обп];ем виде. Рассмотрим следующий числовой пример:

Гд = 0,5 сек, Ti = 0,1 сек, kjk = 26,5 сек,

с двумя вариантами нелинейности:

а) слабая нелинейность

&1 = 0,01, &2 = 0,1, bs = 0,002;

б) сильная нелинейность

bi = 0,1, 62 = 1, 63 = 0,166.

Расчет по формулам первого приближения (18.126) и (18.128) дает авто колебания в виде х = а sin Ы, где для варианта слабой нелинейности

а - 8,14, со = 6 сек~,

а для варианта сильной нелинейности

а = 0,834, со = 6 сек~.

Вычислим теперь высшие гармоники. Для учета второй и третьей гармоник воспользуемся формулой (18.178). Для рассматриваемой в настоящем примере нелинейности F {х, рх) коэффициенты ws.2, подсчитанные по формулам (18.177), оказываются нулями. Поэтому остается только третья гармоника, для которой по формулам (18.177) для данной нелинейности с учетом обозначений (18.121) находим:

гз=--Ьаа-уМ, Sg=-Тфахд. (18.204)

Тогда по формулам (18.179) с учетом тото, что согласно (18.124) Q{p) = {Tgp + i){T + l)p + kik, R{pT={Tip + i)p, находим относительную амплитуду и фазу третьей гармоники:

3 У [ftift-9(7i + 73)w2p4-9w2(l-9rir3w2)2

При указанных выше данных получаем для варианта слабой нелинейности

бз = 0,041, фз = -0,377, а для сильной нелинейности

63 = 0,042, Фз = -0,0384.

1) Нелинейность в данном примере характеризует степень отклонения реальной криволинейной характеристики двухфазного, индукционного йвигателя от прямолинейной

После этого уточняется первая гармоника автоколебаний sin (иЬ. Для этого по формулам (18.183) находим величины добавок Ад и Ад к коэф-фщиентам гармонической линеаризации: :

Ад = -д- ГзЬ1йсобз sin фд- (- + Ъа абд cos фз,

2 / 3 \

Ад= ~д-7з&1асйбзС08фз-/у&2 + М) йбзшфз-

Поэтому новое характеристическое уравнение для определения уточненной первой гармоники будет

тр +1) -Ь (Гз&,а1р -f Ml + hal)\ {Tip -f 1) p -f A;,/c -Ь

+ {4+p)iTiP + i)p0.

Подставляя p = /со и выделяя вещественную и мншлую части, получим

hk- [Гз (1 + &i i) + Ti (1 -ЬMl + М?)] < - {TiAq-f ) to? = О, - (l- Mi + Mn i + A9®i-2i23(l + Mi)co?-r,co?=0.

Эти уравнения решаются тем же методом, что и (18.125), а именное из второго уравнения получаем

2 1 + Мч + Ьзй г + А?

Г1Гз(1 + Ь1а1) + У1-

а из первого

A; = [Гз(+Ml) + Гl(l+Ml + ад)+(2lAg + -)]co

Эти уравнения приводят также к графику % {к) вида рис. 18.23, в. Для приведенных выше числовых значений параметров системы получаем следующие уточненные значения амплитуды и частоты автоколебаний? для слабой нелинейности

% = 8,03, fOi = 5,99 сек-1,

для сильной нелинейности

1 = 0,820, fOi = 5,98 сек-1.

Как видим, сильная нелинейность ) значительно снижает амплитуду автоколебаний (в линейной системе было бы = оо). Этот результат получался выше в решении по первому приближению и подтверждается теперь уточненным решением.

§ 18.6. Частотный метод определения автоколебаний

Здесь, следуя Л. С. Гольдфарбу [32, 121], будем рассматривать простые нелинейности = F (ж), так как в других случаях получаются более сложные графические построения.

Пусть в нелшгейной системе автоматического регулирования выделено, как обьгано, нелинейное звено (рис. 16.1). Разомкнем систему указанным

на рис. 18.38, а образом, причем уравпепие пелипейпого звепа будет

= F (жг), (18.205)

а липейпой части системы -

Q{p)Xs = R ip) Ж2. (18.206)

Замыкание системы соответствует замене

Жз = -(18.207)

Подадим на вход нелинейного звена (рис. 18.38,а) синусоидальные колебания

Xi = а sin at.

(18.208)

На выходе нелинейного звена получим согласно (18.205) вынужденные колебания

х = F (а sin at).

(18.209)

которые можно найти, например, как показано на рис. 18.38, б или в.

Разложим (18.209) в ряд Фурье и сохраним только основную синусоиду (первую гармонику), отбросив все высшие гармоники. Очевидно, что это

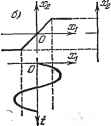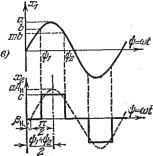Рис. 18.38. -

приближенное представление вынужденных колебаний эквивалентно гармонической линеаризации нелинейностей, рассмотренной в § 18.1. На основании этого для определения первой гармоники вынужденных колебаний величины Жд можно воспользоваться частотным аппаратом, который применялся ранее для линейных систем, следующим образом.

Согласно формулам (18.9) приближенная передаточная функция нелинейного звена с уравнением х = F (ж) будет

W = q (а)

соответственно при наличии гистерезисной петли и при отсутствии ее. При этом выражения q (а) и q (а) определяются формулами (18.10).

Приближенный комплексный коэффициент усиления, или приближенная амплитудно-фазовая характеристика нелинейного звена с уравнением Жа = = F (xj), при наличии гистерезисной петли, следовательно, будет

(а) = q{a) + jq (а), (18.210)