Qi{p)-Q{p) + R{p)(Ag+p),

причем выражение для коэффициента

5 = -,

F ( 1 sin ф) sin ф dip

(18.189)

остается прежним (§ 18.1) с заменой а на Oj. Формулы для добавочных коэффициентов Ад и Ад здесь значительно упрощаются, так как в формулах (18.183) и (18.184) многие члены пропадают, а коэффициент = 0. В результате приходим к весьма простым соотношениям:

Ад = cos Фз, Ад = Згдбз sin фз.

где введено новое сокращенное обозначение hg, причем

li \ -(а81пф)81пЗфз1пфйж, о

Гз = - j F (а sin ф) sin Зф йф.

(18.190)

(18.191)

Из формул (18.179) определяются относительная амплитуда и фаза третьей гармоники:

бз = гз

Л(/Зш)

, Фs = arg

(18.192)

(/Зш)

Таким образом, достаточно просто определяется уточненное периодическое решение для случая однозначной нелинейности F (ж) с учетом третьей гармоники в виде

ж == 1 [sin (Ajt -f- 63 sin (Scojf + Фз)]. (18.193)

Проведем вьгаисление коэффщиептов и Гд по формулам (18.191) для релейных характеристик, где оно представляет некоторые особенности.

Рассмотрим релейную характеристику с зоной нечувствительности (рис. 18.37, а). Входящая под интеграл в формуле для Ад величина производной dFldx будет для этой нелинейности равна нулю везде, кроме двух точек ж = ±&, где она равна мгновенному импульсу, площадь которого равна с (рис. 18.37, б), т. е. величине с, умноженной на дельта-функцию. Выражение sin ф йф при X = а sin ф можно преобразовать к виду

Нпфф=.сгж=.ж=-Гж. 1(18.194)

Поскольку подынтегральное выражение в формуле (18.191) для feg научастке интегрирования (О, л/2) согласно рис. 18.37, д будет нулем везде, кроме одной точки ф = ф;, то эту формулу в данном примере можно переписать в виде

dx = sin Зф, tg ф, {F {а) -F (0)].

Но из рис. 18.37, в имеем

si i = T *Si=yiir рпЗф1 =

ЗЬй2-4ЬЗ

(18.195)

а ИЗ рис. 18.37, а при b

F (а) = с, F (0) = 0.

Окончательно получаем

hs =- (аЬ).

ла* Va2 -62

Формула (18.191) для Гд согласно рис. 18.37, г принимает вид

(18.196)

\ sm3da)) = -cas3%, , Ф1

откуда с учетом соотношений (18.195) находим

4с ( 2 - 462) --

злд Уа-& (а>&).

(18.197)

В частности, для идеальной релейной характеристики из формул (18.196) и (18.197), полагая & = О, получим:

3 = 0 3 = .

(18.198)

Рассмотрим два примера, иллюстрируюп];их процесс отыскания высших гармоник при автоколебаниях, а также уточнения первой гармоники за счет учета высших.

Пример 1. Исследуем следящую систему с нелинейностью типа насыщения, автоколебания в которой в первом приближении ж == а sin coi уже были найдены ранее, в примере 1 § 18.3, в об- /,

щем виде.

Пусть теперь заданы параметры системы: Гв=0,005 сек, То = 0,4 сек, к = 140 сек, kl = 100 сек, fcg = 0,5 сек.

Они удовлетворяют соотношению (18.76). Следовательно, здесь имеет место случай, изображенный на рис. 18.14, б, причем согласно (18.79) и (18.74) кв = 166 сек, /cmin = 125сек. Заданное значение к лежит между ними, что соответствует области наличия двух периодических режимов. Выведенные выше формулы первого приближения (18.70) и (18.71) при этом дают для неустойчивого режима а =

= 2,29 в, сй = 118,2 сек~, а для устойчивого режима а=21,4 в, сй=44,8 сек~}, причем Ям = 7,08 в (в точке сОм рис. 18.14, б).

Наибольший интерес представляет первое (неустойчивое) периодическое решение. Оно указывает границу для начальных условий, вне которой переходный процесс в системе будет расходиться, стремясь к автоколебаниям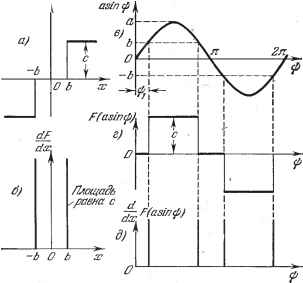

Рис. 18.37.

3 1,/ {Ь-ШеТ1(лТ + 9ЩФ 3 Зсо V (9rfw2-Hl)(9rw2--l)

Фз = .+arctg arctg ЗГсо -arctg ЗГсо.

Вычисление по этим формулам дает

бд = 0,0317, фд = -1,875.

Для уточнения первой гармоники за счет только что вьгаисленной третьей гармоники находим согласно (18.190) добавки к коэффициентам гармонической линеаризации:

Ад = /ig6g cos Фз, Ад = Згдбз sin фд,

подставляя которые в (18.188) согласно (18.68) придем к уточненному характеристическому уравнению

{ТоР +1) (ГвР + 1)р + {к-\. {Т,р +1) кер] (Aq+p) +

+ [к + {Тр +1) hp\ g (аО = О, (18.200)

где аналогично (18.66) имеем:

q = ki при ai<;&, 4

2fei / . 6 , Ь -, Г,-W\ , \ (18.201)

Подставив в уравнение (18.200) р = усо и выделив вещественную и мнимую части, получим два уравнения:

kq (а,) + kAq-lTo + T + ТЛч (i)] - (TAq + )к,(о1=0, [l + keq (а,)1 1 + ( keAq 41 /с) - ToTjol - Тк О.

Эти уточненные уравнения отличаются от прежних уравнений первого приближения несколькими добавочными членами, но способ решения их остается прежним. Из последнего уравнения находим

1 -j-Ав? ( 1) -j- кеАд+ к -

а из первого

(18.202)

к=---- 1- (18.203)

с очень большой амплитудой а = 21,4 е, что практически можно считать неустойчивостью системы в большом. Поэтому уточнение решения с вьгаислением высших гармоник произведем только для первого периодического решения.

Для данной нелинейности (рис. 18.13, а) по формулам (18.191) находим выражения:

Из формул (18.192) и (18.68) получаем относительную амплитуду бд и фазу фд третьей гармоники в виде