Для ТОГО чтобы выходной сигнал достигал уровня ограничения (т. е. чтобы вторая нелинейность участвовала в работе), необходимо вьшолнение условия

Таким обрезом, следует рассматривать входные сигналы с частотой

It ПС

(18.160)

Амплитуда первой гармоники для треугольного сигнала с ограничением имеет вид

4Ь .

(18.161)

Следовательно, первая гармоника сигнала 2 будет

4С2 = 2 sin ((Oif - ф) =

4Ь 4Ь =-sin ф cos ф sin at--sin Ф cos at.

(18.162)

В результате можно записать уравнение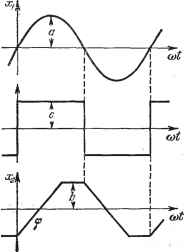

Рис. 18.33.

Рис. 18.34.

нелинейного блока (рис. 18.33) в гармонически линеаризованном виде:

Х2 =

. 26(0

СТТ!

2Ь 81п2ф 2с g

4Ь sinwin

jta ф

, 46 sin ф

па ф

4с Jta

Sin2

Jta со*п

яа (Ofrr

[(18.163)

(18.164)

Характеристическое уравнение всей замкнутой системы при этом полу-чит вид

11+ fcaCt+ ]Ь2СЛ -Ь (feiCi + кЧ) Д > +

+.Г(А;1С1Ч-ад g + AiC2-1 p-HAiO. (18.165)

Для {удобства дальнейших преобразований представим g и - в виде

(18.166)

где Qi и зависят от частоты & , а от амплитуды а не зависят. Будем искать частоту (Оп и амплитуду автоколебаний путем подстановки р = ую в (18.165), что дает:

2=0,

X = 12 -

у = [(hci + кс) ~hc2 - (1 -kci ) (оЗ = 0.

Поскольку а фО, из (18.167) можно найти частоту со: KcQi - [kcQi - (kiCi + kCi) Ql а>1 = 0.

(18.167) (18.168)

(18.169)

Так как в и 2 входит п под знаком тригонометрических функций, решаем это уравнение графически. Его левая часть изображается кривой, показанной на рис. 18.35.

В результате получаются два значения частоты периодического решения: сОд = < ! и

СОп = 2.

Преобразуем уравнение (18.168) к виду с

{kiCi + кс) Qi - /ciC2<?2 -( п- K<iQ2) < = 0.

(18.170)

Отсюда, подставляя значения полученных при Рис. 18.35.

решении уравнения (18.169) частот, можно найти

амплитуду периодического решения сигнала на входе нелинейного звена. Остается определить, которое из двух найденных решений соответствует действительным автоколебаниям в системе. Для этого исследуем устойчивость найденного решения с помощью критерия (18.63). Поскольку согласно (18.167)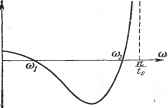

X = Fi(co),

частная производная

() =[-.М] =о,

так как выражение (со) представляет собой левую часть уравнения (18.169), обращающуюся в нуль при со = со д.

Для отыскания представим У в виде

Тогда

У = -12 (а, О)).

/ дУ\ г 1 р , , , 1

да Jn вп е

так как выражение F, (а, со) представляет собой левую часть уравнения (18.170), образующуюся в нуль при со = сОд, а = ап, а частная производная

= -соз.

В результате условие устойчивости автоколебаний (18.63) сводится к требованию

()>0. (18.171)

При отыскании частоты соц автоколебаний по уравнению (18.169) был построен график F (со) = аХ (а, со). Из рассмотрения чтой кривой (рис. 18.35) видно, что условие устойчивости (18.171) выполняется для большего из найденных значений частоты сОп = ci>2. Таким образом, в системе существуют

Нелинейное ввено

Линейная часть

где амплитуда /с-й гармоники ба выражена через амплитуду первой гармоники а, причем коэффи-, Рис. 18.36. . циент 6ft является малой величиной (так как ампли-

туда высшей гармоники предполагается малой по сравнению с адшлитудой первой гармоники). Величину б, играющую в данной задаче роль малого параметра, можно назвать относительной амплитудой fc-й гармоники.

Теперь с учетом конечного числа п высших гармоник искомое периодическое решение (автоколебания) запишется в виде

ж=Ж1+21жй, (18.175)

х-г = % sin cojf

обозначает уточненную по сравнению с (18.173) первую гармонику автоколебаний.

Поскольку амплитуды высших гармоник ба малы, то их вьгаисление можно производить, используя первое приближение периодического решения (18.173), так как использование уточненного решения (18.175) внесло бы в определение ба несущественные малые высшего порядка, но зато привело бы к неразрешимой системе уравнений.

Это чрезвычайно важное (для вычисления высших гармоник автоколебаний) допущение можно иначе сформулировать следующим образом. Считая, что на входе ж нелинейного звена (рис. 18.36) истинное периодическое реше-

автоколебания, параметры которых определяются указанными значениядш частоты п = со 2-

Помимо условия (18.171) для устойчивости найденного решения необхсн димо, чтобы все коэффициенты характеристического уравнения (18.165) были положительными, а именно:

1+2С1-->0, {kiCi + k2C2)q+fciC2~>0,

hcig + {kiCi + k2C2)-:>0, kcqO.

Легко проверить, что все эти условия были выполнены в самом процессе отыскания периодического решения.

§ 18.5. Вычисление высших гармоник и уточнение первой гармоники автоколебаний

Пусть задано дифференциальное уравнение нелинейной системы

Q\p)x + R ip) F (ж, рх) = 0. (18.172)

До сих пор периодическое решение (автоколебания) для нелинейной системы искалось для первого приближения в виде

ж = а sin (ot, (18.173)

что соответствовало приближенному значению первой гармоники периодического решения. Все высшие гармоники при этом отбрасывались ввиду их

малости при наличии в системе свойства фильтра (§ 18.2).

Оставляя в силе это условие, произведем отыскание малых высших гармоник [100], введя отдель- ное обозначение для каждой к-ш гармоники:

ж = ба sin {kwit + фь) (/с = 2, 3, . . .), (18.174)