линейный усилитель-преобразователь вместе с линейным исполнительным устройством -

(Гзр + 1) Ж5 = -F (жз), (18.138)

где Хд = х-г х, а нелинейность F [х задана в двух вариантах.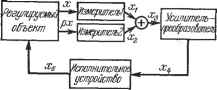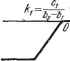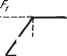

\orctff Af

Рис. 18.25.

Рис. 18.26.

обусловленных разными режимами работы исполнительного устройства -

релейным (рис. 18.27, а) или непре-

с -I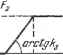

(18.139)

Рис. 18.27.

рывным (рис. 18.27, б).

Будем определять автоколебания приближенно в виде

X = а sin (at,

Xg = 3 (sin at -f- p).

Здесь связь между переменными х и Жд, входящими под знаки нелинейностей, согласно рис. 18.25 идет через нелинейное звено. Следовательно, данная система является системой второго класса (с двумя нелинейными звеньями).

Гармоническая линеаризация нелинейностей согласно § 18.1 дает -

Fi = 91 {а) X, F = ( з) з, (18.140)

где

= 1-+ 1-()) (bi< <b2) (18.141)

и для двух вариантов исполнительного устройства соответственно

<;.-t.-(arcsi +-/ -(-)) №. .,<64). (18.142)

если ищутся амплитуды автоколебаний а и з в -указанных пределах (наличие именно такого автоколебательного режима известно, например, из опыта). Не представляет труда использование выражений q и q, также и для случая а > и Яд > 4 (это ниже для обпцгости будет сделано при изображении графиков 1 и дз)-

Передаточная функция для переменных ж и Хд = х- -{- х запишется теперь согласно (18.136), (18.137) и (18.140) в виде

4i (о) , kv

Жз =

Откуда

ч / [gi (а) - ТффЦ- -f [gi (а) + Это выражение ад {а, ю) будет далее использовано.

(18.143) (18.144)

Составим теперь характеристическое уравнение всей замкнутой системы в гармонически линеаризованном виде. Согласно (18.135) - (18.140) получаем

{Т + 1) {Тр + 1) {Tgp + i)p +

+ kcQ {as) [ТгКр + {q {a) + K)p + ffi (a)l. = 0.

Пренебрегая произведениями постоянных времени при высших степенях р по сравнению с их суммой, что вполне допустимо при рассмотрении низкочастотных автоколебаний (которые здесь и будут иметь место), запишем характеристическое уравнение в виде

(Ti + Т2 + Tg) р + П + Tkjcoq (аз)] +

+ koqz (as) iqi {а) Т + kj р + Kq ( 3) q (а) = 0.

Подстановка р = ja дает:

X = koqz (as) qi {а) - [1 -Ь Tkkq ( з)] = О,

Y = koq {as) [q (а) Т. + к] а - {Т + Т + Tg) а = 0.

Подставив значение kqqi из первого уравнения во второе, поделенное на а, получим (пренебрегая снова произведением TiTi по сравнению с единицей)

=-кок2- (8.145)

Подставив это в пер:вое уравнение {X = 0) и пренебрегая опять-таки произведением Т (Т -Ь Tg) а по сравнению с единицей, найдем

Qii) = ir- (18-16)

Последнее уравнение легко решается графически. Изобразим график {а) согласно формуле (18.141). На рис. 18.28, а это показано сплошной кривой. Пунктирная кривая показывает продод>кение его при а >- Ь.

о Ъ, а

Рис. 18.28.

Путь графического решения уравнения (18.146) показан сплошными стрелками. Этим определяется искомая амплитуда автоколебаний регулируемой величины X. Пунктирные стрелки дают второе решение з (неустойчивое).

Для определения частоты автоколебаний воспользуемся уравнением (18.145). Для этого сначала из формулы (18.144) найдем зависимость 3 (ш) при заданном значении (18.146), что после пренебрежения прежними мальши членами дает

-/1-1-(Г1-ЬГ2+гз)со где значение п берется из графика рис> 18.28, а.

(18.147)

Имея выражение для (яд) [одно из (18.142)], подставим в него полученное 3 (со). Это позволяет построить график (ю) (сплошная кривая на рис. 18.28, б). На тот же графрш наносим правую часть уравнения (18.145) (пунктирная кривая на рис. 18.28, б). Точка пересечения этих двух кривых дает искомое значение частоты автоколебаний как решение уравнения (18.145). После этого становится известной и амплитуда автоколебаний зп на входе усилителя-преобразователя, вычисляемая по формуле (18.147) при найденном значении ю = соц.

Пример 3. Рассмотрим систему, в которой нелинейнъп звеном является логическое устройство (рис. 16.25) с простейшим законом формирования сигнала управления (рис. 16.26). Уравнения системы заданы в виде (16.66) - (16.69).

Установившийся режим в такой системе будет автоколебательным. Искать его будем приближенно в синусоидальной форме

ж = а sin ф, ф = ш.

(18.148)

так как свойство фильтра в данной системе соблюдается. Тогда величины U и j; будут

U = sin (ф - Р), V = cos (ф - -у),

, Y= arctg Гг .

(18.149) (18.150)

В результате процесс изменения и и г; в установившемся режхше будет иметь приблизительно вид некоторого эллипса (рис. 18.29, пунктир). Поэтому включение сигнала Ф в логическом устройстве при данной логике будет

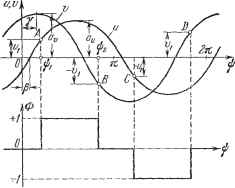Рис. 18.29.

Рис. 18.30.

происходить от величины и (при и = ±1, т. е. в точках Л и С), а выключение - от величины v (при v - ±Ji, т. е. в точках D ж Б; рис. 18.29). Этот процесс во времени (ф = at) изобрантен на рис. 18.30.

Точки включения и вьшлючения определяются на оси абсцисс величинами фх и Фа, причем

sin(4,i-P)=-, со8(фа-т)=-(-).