xi{r)h{t~r)dr, (4.8)

14.3} ЧАСТОТНАЯ ПЕРЕДАТОЧНАЯ ФУНКЦИЯ j61

ПО переходной функции:

:,(t) = xi{0)h{t) + turn по функции веса:

>,(*)= ffj(T) ;(i-T)dT, М

где т - вспомогательное время интегрирования, изменяющееся в пределах от нуля до рассматриваемого текущего момента времени t.

Более подробно методика нахождения переходного процесса при произвольном входном воздействии будет рассмотрена в главе 7.

§ 4.3. Частотная передаточная функция и частотные характеристики

Важнейшей характеристикой динамического звена является его частотная передаточная функция. Для получения ее рассмотрим динамическое звено (рис. 4.1) в случае, когда возмущение / (t) = О, а на входе имеется гармоническое воздействие = cos at, где - амплитуда, а ю - угловая частота этого воздействия.

На выходе линейного звена в установившемся режиме будет также гармоническая функция той же частоты, но в общем случае сдвинутая по фазе относительно входной величины на угол я];. Таким образом, для выходной величины можно записать?

= Хам cos (cof + Щ

Воспользуемся формулой Эйлера и представим входную и выходную величины в виде суммы экспоненциальных функций!

(4.10)

В линейной системе на основании принципа суперпозиции можно рассмотреть отдельно прохождение составляющих х[ и х[. Кроме того, можно легко показать, что достаточно рассмотреть прохождение только составляющей х[, которая в выходной величине дает составляющую ж. Соотношение между составляющими х и х получается таким же, как между х\ и х. Поэтому в дальнейшем рассмотрении воспользуемся символической записью ) cos cof = eJ*. Тогда

(4.11)

Символичность этой сокращенной записи] заключается в отбрасывании составляющих с множителем е~.

Для нахождения соотношения между входной и выходной гармоническими величинами звена воспользуемся его дифференциальным уравнением

в виде

n+T. + x, = k,x, + k,.

*) Иногда употребляют символическую запись sincoi=e *.

Из выражений (4.11) определим производные: .

Подставив значения входной и выходной величин и их производных в исходное дифференциальное уравнение, получим:

Т1 (jaf Х2ме( *+*) + Г1/сйХ2ме( *+*> + Х2ме( *+*> = hXie<t + 2/(0X16 *,

откуда после сокращения на общий множитель е? * найдем:

Это выражение* называется частотной передаточной функцией звена. Таким образом, частотная передаточная функция W {jai) представляет собой комплексное число, модуль которого равен отношению амплитуды выходной величины к амплитуде входной, а аргумент - сдвигу фаз выходной величины по отношению к входной:

oiJ.)=\WiJ.)\ = , I

arg W (/со) = !). J

В более общей формулировке для входного сигнала любого в ида частотную передаточную функцию можно представить как отношение из ображений Фурье (частотных изображений) выходной и входной величин:

что непосредственно вытекает из формулы (4.1) при переходе от изображения Лапласа к изображению Фурье; следовательно, частотная передаточная фушция легко получается из обычной передаточной функции подстановкой р = /со.

Частотная передаточная фзшкция звена есть изображение Фурье его функции веса, т. е. имеет место интегральное преобразование

W (/(0) = j W (f) e-i t dt. (4.15)

Частотная передаточная функция может быть представлена в следующем виде:

. W (усо) = А (со) ei* = f/ (со) + jV (со), (4.16)

где А (со) - модуль частотной передаточной функции, if (со) - аргумент или фаза, и (со) и V (со) - вещественная и мнимая составляющие частотной передаточной функции.

Модуль частотной передаточной функции находится как отношение модулей числителя и знаменателя. Для рассмотренного выше примера (4.12)

Аргумент или фаза частотной передаточной функции находится как разность аргументов числителя и знаменателя. Для (4.12) имеем:

,i,(co) = arctg--arctg.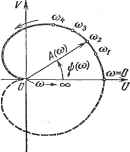

X (/со) = J ж (г) е- *

функция времени х (t) преобразуется в функцию частоты X (/to). Это означает, что функция времени представляется в виде бесконечной суммы бесконечно малых по величине векторов, вращающихся на комплексной плоскости с различными угловыми скоростями (частотами) ю. Эта сумма определяется формулой обратного преобразования Фурье

с+оо

где с - абсцисса абсолютной сходимости.

Так как функция времени является вещественной, то каждому элементарному вектору X (/со) е5 *й(й, вращающемуся против часовой стрелки (со > 0), должен соответствовать элементарный сопряженный вектор X (-/со) е~5 *й(й, вращающийся по часовой стрелке (ю -< 0). В этом случае сумма таких векторов в любой момент времени будет всегда вещественной. Поэтому интегрирование в формуле обратного преобразования Фурье должно вестись по всем частотам от -оо до -j-oo.

Для нахождения вещественной и мнимой частей частотной передаточной функции необходимо освободиться от мнимости в знаменателе путем умножения числителя и знаменателя на комплексную величину, сопряженную знаменателю, и затем произвести разделение на вещественную и мнимую части. Для (4.12)

Для наглядного представления частотных свойств звена используются так называемые частотные характеристики.

Амплитудно-фазовая частотная характеристика (а. ф. х.) строится на комплексной плоскости. Она представляет собой геометрическое место концов векторов (годограф), соответствующих частотной передаточной функции W (/ю) = U (со) -Ь jV (ю) при изменении частоты от нуля до бесконечности (рис. 4.7). По оси абсцисс откладывается вещественная часть и (со) = В.е W (/ю) и по оси ординат - мнимая часть V (ю) = 1т W (/со). Для каждой частоты на комплексной плоскости наносится точка. Полученные точки соединяются затем плавной кривой. Около нанесенных точек можно написать соответствующие им частоты (Oi, (Oj, (Og и т. д.

А. ф. X. может быть построена как для положительных, так и для отрицательных частот. При замене в частотной передаточной функции +ю на -ю Рис. 4.7. получится сопряженная комплексная величина. Поэтому а. ф. X. для отрицательных частот может быть построена как зеркальное изображение относительно вещественной оси а. ф. х для положительных частот. На рис. 4.7 а. ф. х. для отрицательных частот показана пунктирной линией.

Отметим, в чем заключается смысл положительных и отрицательных частот. При помощи преобразования Фурье