После подстановки р = /ю получаем: X = кк - [Гз (1 -Ь М) + 1 (1 + Ъа + Ъф)] = о, У = (1 -Н + Ьзй ) и - TsT-, (1 + М = О-

(18.125)

Рассмотрим при этом влияние параметра к (общего коэффрщиента усиления регулятора). Второе из уравнений (18.125) дает

ад=-щ--. (18.126)

Из (18.121) видно, что Ь > Ь. Поэтому полученная формула дает зависимость амплитуды а от частоты а) искомого периодического решения в виде графика, показанного на рис. 18.23, б, где

Далее, первое из выражений (18.125) при a) = cuiiHa = anC использованием второго приводит к формуле для параметра к, влияние которого рассматривается:

k={l + bia)(l + Tla>l)i>l. (18.128)

По этой формуле, используя предыдущие результаты, получаем график зависимости амплитуды автоколебаний от величины параметра к, показанный на рис. 18.23, е.

§ 18.4. Нелинейные системы второго класса

Нел1шейные системы второго класса - это системы с несколькими нел1шейными звеньями или же с одним нелинейным звеном, когда под знаки нел1шейных функщий входят две или более переменных, связанных между собой лршейньши передаточньши функциями или нелинейньши уравнениями. Обычный прием приближенного решения, излагаемый ниже в примерах 1-3,

Подставляя это в (18.119), получаем следующее уравнение двухфазного двигателя (для колебательных процессов):

ITg (1 + V) Р + {1 + b2a + bga)] X = kU, (18.120)

вместо обычного линейного {Тр -{- 1) х = kU, где

Ts=i, h = , bi = , h=2bi + , Ьз = -. (18.121)

Здесь а обозначает амплитуду колебаний угловой скорости двигателя х = Шдв, Далее, скорость перемещения регулирующего органа pg с учетом передаточного числа редуктора и с обозначением (18.118) будет

р1 = кх. (18.122).

Уравнение регулируемого объекта и уравнение чувствительного элемента регулятора возьмем соответственно в виде

{Tip -Н 1) Ф = -hh и = йф, (18.123)

где ф - отклонение регулируемой величины.

Характеристическое уравнение всей замкнутой системы будет

[Гз (1 + Ьа) p + (l + b2a + b)] {Тр + 1) р + кк = О, (18.124)

справедлив при соблюдении условия фильтра, оговоренного в § 18.2, для всех передаточных функций, связывающих указанные переменные. Если это условие не соблюдается, применяется специальный прием решения, изложенный ниже в примере 4.

Пример 1. В предыдущем параграфе рассматривалось влияние нелинейности прршода, а затем влияние квадратичного трения по отдельности. Рассмотррш теперь совместное действие нелинейности привода и квадратичного трения. Момент трения при этом описывается нелинейным членом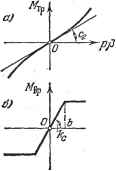

со

Рис. 18.24.

F (ж), как в уравнении (18.90), или, что то же самое, графиком на рисунке 18.24, а. Нелинейный привод пусть имеет характеристику типа насыщения (рис. 18.24, 6).

Тогда уравнение двигателя и управляемого объекта вместо (18.90) прршет вид

(Го/? -Н 1) ж + {х) = cFi а,), X = рР, (18.129)

где Fi (i ) = Мвр и определяется графиком рис. 18.24, б.

В данном случае получается нелршейная система второго класса. Приближенно полагаем, что при автоколебаниях

ж = а sin at, i = Аа sin {at -\- R)i

(18.130)

где A (ш) и В (ш) - модуль и аргумент амплитудно-фазовой характеристики линейной части, получаемой из уравнения (18.67), которое согласно (18.129) надо умножить на р. В результате получим

к , кТ

(Гв/С0-1)/С0

Отсюда

.2 , к-ШбТг>(й-

(l-fH 0)2)0)2

(18.131)

что изображено графически па рис. 18.24, е.

Поскольку в уравнение (18.129) переменные ж = /?р и г входят раздельно, то и гармоническую линеаризацию можно производить для канчдой из них отдельно. К нелинейности в левой части уравнения (18.129) пррше-няем формулы из прежнего примера 3 (с квадратичным трением), а к нелинейности в правой части - формулы (18.65) и (18.66), в которых, в соответствии с (18.130), вместо а подставляем Аа. В результате нелинейное урав-

некие (18.129) пршншает вид

q= ki = ckc 2к,

arcsm

при аЪ, Ъ , Ъ

аА (ш) аА (ш)

. аА (со) J /

(18.132)

(18.133)

причем А (со) определяется формулой (18.131) или графиком рис. 18.24, е.

Из уравнений (18.132) и (16.53) получаем гармонически линеаризованное характеристическое уравнение замкнутой системы в ;виде

(Пр + 1)(ГоР + 1+)р+[(гвР+1)М + ]д(а)=0. Следовательно, после подстановки р = /со, находим:

X = kq (а, со) - Го + + kjq {а, со)

8V г

со2 = 0,

l+keq{a, со).

со-ГоГзСоЗ = 0,

откуда получаем:

д(аи, со,) = -1-(ГоГ,с4-1 ) , к =

g (On, СОп)

(18.134)

Из первого уравнения легко определяются все возможные значения амплитуды и частоты сОп следующим образом.

Задаемся каким-нибудь значением сОд. Из графика на рис. 18.24, е находим для него величину А (сОд). По формуле (18.133) строим кривую qia, СОп), показанную на рис. 18.24, г.

Обозначим далее правую часть первого из уравнений (18.134) через z (при переменной а вместо а):

.(а,СОп)-

и проведем согласно этой формуле на том же рис. 18.24, г прямую z {а, (о ). В точках пересечения получаем искомые значения амплитуды , а также и значения д {а , соц). После этого по второй из формул (18.134) подсчитаем величину параметра к.

Проделав такую же операцию для различных значений со и получая каждый раз и к, сможем построить и здесь графики, подобные тем, которые получались в предыдущих прршерах. Амплитуда колебаний угла о будет Р = п/<Ип- При этом согласно (18.134) из условия положительности вели-

ЧРШЫ q ( п! <Вп) должно быть СОп >

Пример 2. Пусть в системе, функциональная блок-схема которой изображена на рис. 18:25, регулируемый объект описывается уравнением

рх = кох, (18.135) измеритель 1 - нелинейный (рис. 18.26) -

{Tip + l)Xi = Fi (х), (18.136) измеритель 2 - линейный -

(Тр -Н 1) Ж2 = крх, (18.137)