изобрадгенная на рис. 18.21, б. Здесь возможен только автоколебательный процессе; область устойчивости равновесного состояния, имевшаяся на рис. 18.21, а, пропадает.

Как видим, зона нечувствительности имеет стабилизируюш;ее значение для релейной системы автоматического регулирования, причем ширина области устойчивости (О Л kaiv) согласно (18.108) пропорциональна ширине зоны нечувствительности 26. Сравнение данного решения, учиты-ваюв];его инерционность регулятора Tg, с решением без учета показывает принципиальную важность учета этого фактора. Например, для характеристики вида рис. 18.20, в без учета получится только устойчивость {а = 0) при любых числовых значениях параметров (что нереально), а с учетом - только автоколебания (рис. 18.21, б). Для характеристики вида рис. 18.20, б вместо неограниченной области устойчивости (без учета Т) получается ограниченная и возникает еш;е область автоколебаний с большой амплитудой

при одновременном существовании устойчивости в малом (рис. 18.21, а).

Далее, в третьем частном случае, когда характеристика реле чисто гистерезисная (рис. 18.20, г), т. е. = -6 = -Ь, из (18.99) имеем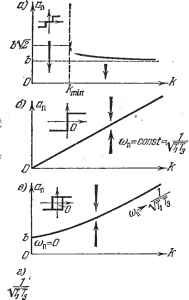

При этом из (18.102) находим

(18.110)

а из (18.103)

яЬЮд(1-]-Гы)(1-]-Г§ы)

(18.111)

(18.112)

По этим формулам построены кривые на рис. 18.21, в ж г, определяющие амплитуду и частоту периодического решения в зависимости от величины параметра к. Устойчивость периодического решения определим здесь по методу осреднения периодических коэффициентов. Для вычисления коэффициента % (а) согласно (18.60) нужно знать производную от и по X, которая, однако, обращается в бесконечность при х = Ь, когда рх>0, и при X = -Ь, когда рх <. 0. Чтобы избежать этого, заменим заданную характеристику (рис. 18.20, г) новой (рис. 18.22, а), из которой заданная получается предельным переходом (другой способ, с дельта-функцией, см. в § 18.5,

рис. 18.37). Для характеристики на рис. 18.22, а при изменении величины аг

по закону X = а sin at (рис. 18.22, б) производная -принимает значения,

показанные на рис. 18.22, в, где

Рис. 18.21.

ф1 = arcsin -

фа = arcsin

(18.113)

Осредненное ее значение (18.60) согласно рис. 18.22, е с предельным пере-

ХОДОМ К заданно,!! характеристике {h -> 0) будет

2с №2-я))!)

2- №2-1)

так как h = а sin фа - sin ip.

Обозначив = 1 + Аф и взяв производные от числителя и знаменателя по Аф, получим

X(a)=lim-п--гтт = --Д=-. (18.114)

Итак, для исследования устойчивости получаем следующее характеристическое уравнение:

ТТдр + {Ti + Тд)р+р + kJcX {а) = 0.

(18.115)

Условие устойчивости периодического ре шения, следовательно, по критерию Гурвица будет

Подставив сюда ОС (а) из (18.114) и значения 4 и Л из (18.111) и (18.112), убедимся, что оно выполняется. Следовательно, в системе в) будут устойчивые автоколебания а; = sin п, амплитуда и частота которых определяются графиками рис. 18.21, в ж г или формулами J;; (18.111), (18.112).

Пример 6. Пусть в той же системе характеристика реле имеет простейший вид Рис. 18.22.

рис. 18.20, е, но имеется постоянное по времени

запаздывание т. Тогда согласно (18.110), где 6 = 0, уравнение нелинейного звена будет

В результате получим характеристическое уравнение системы

{Tip + 1) {Т,р +i)p + kike--P=0.

Подстановка р = ую с учетом выражения e J = cos тсо - ; sin то даст два уравнения:

X = cos тсо - {Ti -Ь Тз) 0)2 = О,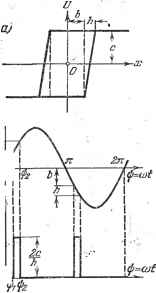

У = sin ТО) 4-О) - Г1ГзО)3 = О,

из которых находим два соотношения:

(ri-fr3)o) tgTO)n=l-rir30): 4cfcift

On =

зивп ]/1 + (Г! -Ь Г!) 0)2 + Т\

Первое из них определяет частоту (решается графически), а второе - амплитуду автоколебаний в зависимости от коэффициента усиления регулятора Л и от других параметров системы.

Заметим, что во всех случаях, рассмотренных в примере 5 и в данном примере релейной системы, через Сц обозначалась амплитуда автоколебаний

величины X. Амплитуда же автоколебаний се регулируемой величины 6 (температуры) бу-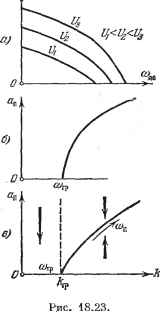

6 =

Пример 7. Рассмотрим систему автоматического регулирования с приводом, регу-лируюш;его органа в виде двухфазного двигателя переменного тока. Характеристика этого двигателя для разных значений управляющего напряжения U имеет вид, представленный на рис. 18.23, а.

Линеаризуя характеристики, обычно считают

М = си - cd)

(18.116)

Но это справедливо в первом приближении только для левого участка характеристики. Если же используется большая часть характеристики, то необходгшо учесть ее нелинейность. Имея в виду, что на рис. 18.23, а с увеличением (Оде коэффициент Ci уменьшается, а коэффициент увеличивается, примем для описания этой характеристики вместо (18.116) следующее нелинейное выражение:

(абсолютные значения дв в коэффициентах поставлены потому, что (Ода меняет знак, а сами коэффициенты должны оставаться полонштельными числами). Аналогично можно подбирать и любой другой более подходящий нелинейный закон для описания характеристик двигателя.

Введем для дальнейшего обозначение

X = сйдв. (18.118)

Тогда дифференциальное уравнение двигателя

и - сх - С41 а; j ж

1 + сз1

(где / - момент инерции всех вращаемых двигателем масс, приведенных к валу двигателя) можно записать в виде

+Jcs\x\~ + CX-{- (СаСз + С4) \х\х-{- СдС.Х = CiU.

(18.119)

Здесь имеем три нелинейные функции:

Fx=\x\, F, = \x\x, Гармоническая пх линеаризация по правилам § 18.1 дает:

F, = х.

4а dx

Зл dt