Следовательно, после подстановки р = ](и получим X=kikg (а)- [Т-ТТоЩ {а) + ТоЯ (а) + kjtjq (а)] О,

1 ~ Toq (а) со -f kikeg (а) - kik

q(a)

со -

q (с)

0)3 = 0.

Для исследования влияния параметра к на собственные колебания данной системы выразим величину к из каждого уравнения по отдельности:

4{а) кл{а) -

kxq (а) J ftjg (a)

(18.97)

L g (a) /c5 (a) J

-(-rA)co-ico3. (18.98)

Задаваясь разными значениями a = a, для каждого из них по eithm уравнениям строим две кривые к (со) (рис. 18.19, б). Точка их пересечения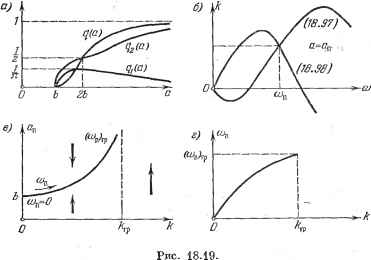

дает соответствующие значения Юц и Л. В результате можно построить графики (рис. 18.19, е и г) зависимостей амплитуды и частоты сод периодического решения от параметра к (каждое построение на рис. 18.19, б дает по одной точке на каждом из графиков рис. 18.19, е и г).

При й = оо, как видно из рис. 18.19, а, имеем д (а) = д (а) = 1 и Яг (а) = 0. Поэтому из выражений X (юп) = О и У (сОд) = О находим:

Ы2 1 + Мв. ГР--у-у-

кгр -

(1 + fctfce) (ГоЧ-Гв+ГвМб)

причем вдоль кривой на рис. 18.19, в частота сОп изменяется в интервале

О < СОп < (Сйп)гр-

Пример 5. Пусть имеется релейная система регулирования температуры (рис. 1.35), описываемая согласно § 16.1 уравнениями (с дополнитель-ньш учетом постоянной времени привода Тд):

(Tip + 1) е = - х = кВ, (Тдр + 1) pip = ksU, U = F (х).

где X - ток В диагонали моста (управляющей обмотке реле), а F {х) - характеристика реле, изображенная на рис. 18.20, а. В следующем примере произведем также учет не гистерезисного, а временного запаздывания реле.

Рис. 18.20.

Гармоническая линеаризация характеристики реле рис. 18.20, а согласно формулам (18.9) и (18.15) дает

(18.99)

На основании написанных уравнений получаем следующее характеристическое уравнение данной замкнутой системы:

{Tip+ 1) (Тдр + 1)р + кк [д (а) - р

= 0,

к - ккд.

Отсюда после подстановки р = усо получаем выражения:

X=hkg{a)~{Ti + rs)a=0, Y =

ikg{a)~{Ti + rs)ti)=0, . 1 - kik -] (0 - 130)3 = 0.1

(18.100)

Исследуем влияние параметра к на устойчивость и автоколебания данной системы.

Из (18.100) имеем

9( п) (7i + 3s)con

откуда после подстановки (18.99) находим

(18.101)

(18.102)

Тогда из второго уравнения (18.100) с учетом (18.99) получаем

я(1-Г1Гзсо)соп

\ да )п~ аУБ V 2 j / дХ \ >0 при а<:ЬУ2, [ да }n\Q jjpjj а>ЬУ2,

eajn- isM/непо-

следовательно, нижняя ветвь кривой на рис. 18.21, а соответствует неустойчивому периодическому решению, а верхняя - устойчивому (автоколебания).

Пусть в другом частном случае характеристика реле имеет идеальный вид (рис. 18.20, в), т.е. = = Ъ = 0. Здесь получается прежнее постоянное значение (18.106) и согласно (18.107) - прямолинейная зависимость

На основании формул (18.102) и (18.103) можно построить графики для амплитуды в зависимости от параметра к по точкам, соответствующим различным значениям частоты как это делалось в предыдущих примерах. При этом, исходя из положительности к, согласно (18.103) нужно задавать значения соц в интервале

0<cuS<y. (18.104)

Рассмотрим частные случаи.

Пусть реле имеет характеристику вида рис. 18.20, б, где = = Ъ. Для этого случая из (18.99) получаем:

?=1&-V = 0. (18.105)

Поэтому второе из уравнений (18.100) дает постоянное значение частоты периодического решения

<:=- (18.106)

Подставляя его в первое уравнение (18.100), с учетом (18.105) находим

n(Ti+Ts] (6<Сп<оо). (18.107)

Здесь к = оо в двух случаях: = b ж = оо. Найдем kiin из условия равенства нулю производной к ио а.

-n = 4g (18.108)

при = b У2.

Соответствующий график зависимости амплитуды от параметра к изображен на рис. 18.21, а. В этом частном случае релейной характеристики (рис. 18.20, 6) для исследования устойчивости воспользуемся критерием (18.63), для которого предварительно находим: