найденного периодического решения. Это и показано условно вертикальными стрелками на рис. 18.16, б.

Легко проверить, что значение к (18.88) совпадает с границей устойчивости линейной системы без сухого трения. Следовательно, добавление сухого трения несколько расширяет область устойчивости системы, но весьма своеобразно, а именно: неустойчивость найденного периодического решения означает, что при Л > Лгр и при выполнении условия (18.89) система может быть устойчивой в малом (при начальных условиях, которые дают начальную амплитуду собственных колебаний системы в переходном процессе, лежаш;ую ниже кривой на рис. 18.16, б). Однако система неустойчива в большом (при начальных амплитудах собственных колебаний выше этой кривой). Последнее можно объяснить физически тем, что при больших амплитудах и соответственно при больших скоростях движения демпфируюш;ее влияние силы сухого трения, которая сохраняет одну и ту же величину при любой скорости, становится несуш;ественным, вследствие чего система оказывается неустойчивой, как и при отсутствии сухого трения.

При невыполнении условия (18,89) требуется исследование обоих уравнений (16.52) совместно (это будет уже нелинейность второго класса, так как она затрагивает обе величины: входную 1я и выходную р). При этом

колебания угла Р будут происходить с останбвка-ми. Это - задача более сложная.

Пример 3. Пусть теперь в той яте системе действует не сухое трение, а сопротивление движению объекта, пропорциональное квадрату скорости, с линейной составляющей рис. 18.17, а. Уравнение управляемого объекта с двигателем имеет в этом случае вид (16.63). Перепишем здесь его иначе по аналогии с предыдуш;им примером: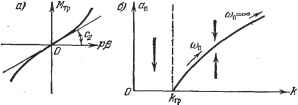

Рис. 18.17.

(ТоР + l)x + F{x) = ki, X = рр, F {х) = кх sign X,

(18.90)

Полагая х = а sin а>1, по формулам гармонической линеаризации (18.10) получаем

g = j fcga sin ф (sign sin ф) sin ф йф =

л 2я

Следовательно,

Р{х)

8kga

Составив, как и раньше, характеристическое уравнение, приходим к выражениям:

X=-hk~(To + T + hkeT-l

Г,)(02=0,

§ 18.3] ПРИМЕРЫ ИССЛЕДОВАНИЯ НЕЛИНЕЙНЫХ СИСТЕМ!ПЕРВОГО НЛАССА 563

откуда находим:

к = {П< + 1), ап = -№ -1-ВД. (18.92)

Граничные значения сОд и к совпадают здесь с прежними (18.88), но они соответствуют уже не = оо, а = 0. В результате получаем график для определения амплитуды и частоты периодического решения, изображенный на рис. 18.17, б.

Поскольку здесь

().< . ().> - (f ).< . (f ).< .

то критерий (18.63) выполняется. Поэтому найденное периодическое решение устойчиво. Следовательно, квадратичное трение приводит к автоколебаниям в той области параметров, где система без этого добавочного трения была бы неустойчивой. Это объясняется усилением демпфируюпего действия квадратичной силы трения при увеличении амплитуды (и скорости) колебаний, что препятствует неограниченному раскачиванию системы. Заметим, что переход закона сопротивления движению объекта от линейного к квадратичному при больших скоростях отражает реальные явления.

Амплитуда и частота автоколебаний определяются здесь графиком рис. 18.17, б или формулами (18.92), причем амплитуда колебаний угла 3 будет Of, = ац/сйц.

Пример 4. Пусть в той же следяпей системе требуется учесть влияние зазора в механической передаче между двигателем и управляемым объектом (схематически он показан на рис. 16.20) при линейной характеристике двигателя и при линейном трении. В колебательных процессах, которые здесь рассматриваются, зависимость между углами поворота р (после зазора) и pi (до зазора) будет иметь нелинейный вид, показанный на рис. 16.20, б, где b - половина ширины зазора. КрОме этой нелинейной зависимости здесь присутствует вторая нелинейность (16.54). Полагая, что момент инерции управляемого объекта велик по сравнению с приведенньш моментом инерции двигателя, будем считать в уравнении (16.54) Ti = 0.

Первая нелинейность (рис. 16.20, б) после гармонической линеаризации при Pi = а sin at согласно формуле (18.30) принимает вид

Р=[?( )-р]Рь (18.93)

где q (а) и д (а) определяются по формулам (li8.27), в которых надо считать к ~ i (так как характеристика рис. 16.20, б имеет наклон 45°), а именно:

q = m + b + h2) = < = -S{l-) (18-9)

причем

ф1 == arcsin (l--). (18.95)

Вторую нелинейность (16.54) запишем в виде F (pPi, pj) = AtjV Она подвергается гармонической линеаризации по формулам (18.11) такжо при Pi = а sin at.

Зависимость между углами pi и р показана на рис. 18.18. При этоМ из; нижнего графика и из формул (16.54) видно, что

pPi) = VPi-bpPi

и (учитывая, что = 0)

Условие отсутствия постоянной составляющей здесь выполняется, а третья изТформул (18.11) принимает вид.

2з1 л/2

§1 (а, со) = j (аю cos ф) cos ф йф 4- То{-ш- sin ф) соз.ф йф 4-0 о

Зя/2 2я

rf j Го( -а< 81пф)со8фйф4- j Го ( -асй2 81пф) созфйф ;

Я-ф!

2л-11)1

аналогично определяется и g-g ( <j5)- Произведя интегрирование и сравнив результаты с выражениями (18.94), получаем

§1 (fl, со) = (О - g (а) Гo

где д (а) то же, что в формулах (18.94). В результате вместо нелинейного уравнения (16.54) при = О имеем

[д {а) ГоР + 1 - q ( ) Го ] = кг, д2(а) = -(-- + ф1--siп2фl) ,

(18.96)

причем q (а) и ф те же, что и в (18.94) и (18.95). На рис. 18.19, а изображены графики для величин коэффициентов g (а), q (а), q (а).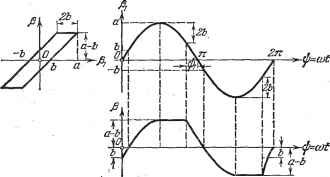

Рис. 18.18.

На основании (18.93), (18:96) и линейной части (16.53) приходим к характеристическому уравнению

(УвР +1) [2 {а) ГоР +1 - д (а) ТоЩ р +

+ kd{Tp+i)keP + k] q{a)

q(a)

= 0.