справедлив график на рис. 18.14, а, а для системы с параметрами

hh>yi + (18.76)

- на рис. 18.14, б.

Исследуем устойчивость найденного периодического решения по критерию (18.63). Согласно (18.66) частота со не входит в коэффициенты. Поэтому в выражении (18.45) для кривой Михайлова функции X (со) и F (со) совпадают с (18.69).

Найдем производные:

() =-2[Го + гв + гвд(ап)]о)п=-2ГоЮ (1 + ПО<0, 1-) =l + hq (йп) -ЗГоW = -2ГоГеО) < о, () =<.-r.*,(A) =i (*) < ,[ (18.77,

так как согласно рис. 18.13, б производная dq/da отрицательна.

Легко проверить, что при со > со, где сощ определяется формулой (18.73), критерий (18.63) удовлетворяется, а при со <; со не удовлетворяется. Отсюда делаем заключение, что все периодические решения на рис. 18.14, а устойчивы (т. е. соответствуют автоколебаниям). Вертшсаль-ными стрелками там показано, что переходные процессы с большими и меньшими амплитудами сходятся к данному периодическому процессу. На рис. 18.14, б только верхняя ветвь кривой (выше точки со) соответствует устойчивым периодическим решениям, т е. автоколебаниям, а нижняя (соад -f- сое) - неустойчивым.

Как уже отмечалось, через Яц здесь обозначена амплитуда колебаний величины t . Чтобы узнать амплитуду ар автоколебаний регулируемой величины р, надо воспользоваться уравнением (18.65), откуда

а, = ---ап= fJOn (18.78)

как модуль соответствующей передаточной функции при р = /сОп, умноженный на йд. При этом величины а и сОп определяются графиком рис. 18.14, а или б.

Учитывая, что q (а) = при а = Ъ (см. рис. 18.13, б), найдем по формуле (18.71) с подстановкой сод = сов из (18.72) величину к, отмеченную на рис. 18.14:

(18-7>

Точно такое же значение к является границей устойчивости для линейной системы, когда уравнение управляемого объекта с двигателем вместо (18.65) имеет линейный вид {Тр -j- 1) рР = /сг. Отсюда могкно сделать вьшод о том, что в случае (18.75), для которого имеет место график рис. 18.14, я, данная нелинейная система сохраняет устойчивость в той же области, что и лицейная система, но она обладает еще установившимся автоколебательным режимом там, где линейная система неустойчгша. Следовательно, ограничение линейной характеристики типа насыщения в двигателе (рис. 18.13, а) препятствует раскачиванию системы, которое получается при А; > /сщ в линейной системе. Это наблюдается и на практике.

В случае же (18.76), для которого график, определяюпрш автоколебания, имеет вид рис. 18.14, б, автоколебания могут уже появиться при к <С кв (но > йщ), т. е. раньше наступления границы устойчивости линейной системы. Но в этом случае, как видно из рис. 18.14, б, при малых начальных амплитудах переходного процесса (ниже кривой сОмЮб) сохраняется еш;е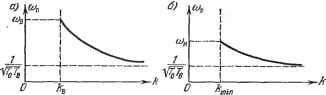

Рис. 18.15.

устойчивость равновесного состояния. Здесь в области параметров < <Ск <Z кв (рис. 18.14, б) имеется как бы два предельных цикла (рис. 16.14, в), а в области А;в < А; < оо - один.

Случай, изображенный на рис. 18.14, б, называется жестким возбуждением автоколебаний. Такое возбуждение автоколебаний раньше наступления границы устойчивости возможно, как видно из (18.76), только при достаточно большом kg, который, по существу, является коэффициентом

гибкой обратной связи.

Рис. 18.16.

При отсутствии такой связи указанное явление не имело бы места.

На рис. 18.15, а ж б даны граф1ши для величины частоты автоколебаний ./( (Оц в зависимости от пара-

метра к соответственно для случаев, изображенных на рис. 18.14, а и б.

П ри м е р 2. Рассмотрим теперь следящую систему с линейной характеристикой привода, но учтем сухое трение совместно с линейным (рис. 18.16, а). Уравнение управляемого объекта с двигателем имеет при этом вид (16.52). Здесь возможны два случая: 1) колебания без остановок, когда обеспечиваются условия первого из уравнений (16.52); 2) колебания с остановками, когда действуют попеременно оба уравнения (16.52). Рассмотрим первый случай и определим условия его существования.

Итак, записываем первое из уравнений (16.52), поделив его на с, в виде

£2

С условием, что

гя>- при рр = 0.

Обозначим X = рр. Тогда это уравнение будет

(ГоР + Г)х + Р{х)= kii,

(18.80)

(18.81)

(18.82) (18.83)

F (ж) = k sign х.

Выражение (18.84) представляет собой известную формулу линеаризации сухого трения с помопью вибраций. Найдем условия, при которых она здесь справедлива. Согласно (18.81) и (18.82) имеем

I Jfl рр=о = откуда

>

acu>-Z- или apCu2>A-, (18.85)

что И является условием, при котором справедливо дальнейшее рейение.

Характеристическое уравнение всей замкнутой системы согласно (18.82), (18.84) и (16.53) получает вид

(Тр + l)p + ki (Тр + 1)к,р + кк + (ТоР + 1) (Тр 4- 1) р = 0.

После подстановки р = /со получаем

= - (+ kikeT + T, + To)(i>=0,

, /1. ? (18.86)

( + e +1) - = 0-

Чтобы исследовать влияние коэффициента к на динамику системы, выразим из этих двух уравнений величины к ж через

Заметим, что = 00 при

(co )p = i±, к = ±(1 + 4-). (18.88)

Изменяя СОп в интервале (сйп)гр + оо> строим по формулам (-18.87) график - f (к), представленный на рис. 18.16, б. Условие, при котором справедливо это решение, было выражено неравенством (18.85). Подставив в него значения а = и со = из (18.87), приводим его к виду

где

byn+AkikToTi-To.

Для исследования устойчивости найденного периодического решения на основании (18.86) находим

().> . (). . (f).< . (f).< -

Критерий (18.63) при этом не выполняется, что означает неустойчивость

Поскольку движение предполагается без остановок, то нелинейную функцию (18.83) подвергаем гармонической линеаризации, как релейную характеристику, и на основании формулы (18.18), полагая х=а sin получаем

i(x) ix, (18.84)

где а - амплитуда колебаний скорости х = ]э3. Амплитуда колебаний самого угла 3 при этом, очевидно, будет