(18.64)

выполнения критерия Гурвща для многочлена

где D (р) - левая часть гармонически линеаризованного характеристического уравнения (18.33) при а = а и & = а. При этом если D [р) имеет

пятую или впестую степень, достаточно убедиться в положительности коэффициентов Di (р).

Устойчивость равновесного состояния системы. Приведенные в начале данного параграфа гармонически линеаризованные уравнения нелинейной системы годятся только для колебательных процессов, определяемых периодическими решениями, и для колебательных переходных процессов в непосредственной близости от указанных периодических решений. Поэтому, строго говоря, с П0М0ПЦ.Ю этих приближенных уравнений можно анализировать только сами периодические решения и их устойчивость или неустойчивость при малых отклонениях от исследуемого колебательного режима, что выше и делалось.

Практически же из анализа полученных приближенных уравнений нелинейной системы часто можно делать значетельно более широкие выводы. В частности, можно оценивать устойч1тость системы в тех областях ее параметров, в которых периодические решения отсутствуют вовсе.

Пусть, например, определено, что периодическое решение, амплитуда которого показана на рис. 18.5, а , устойчто (оно соответствует автоколебаниям). Условимся факт устойч1шости периодического решения обозначать

Рис. 18.11.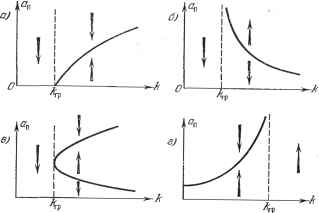

Рис. 18.12.

на графике вертикальными стрелками, сходяш;имися к данному периодическому решению (рис. 18.12, а). Этим обозначением: иллюстрируется то, что переходные процессы с обеих сторон (т. е. с большими, чем Яц, и с меньшими, чем йц, начальными амплитудами) сходятся к автоколебательному процессу с амплитудой а- Пусть в данном случае к обозначает коэффщиент усиления регулятора. График рис. 18.12, а показывает, что в системе возникают автоколебания при к > Лгр. Естественно сделать отсюда вывод о том, что в обла-

сти о <; А; <; игр (где нет периодического решения) данная система регулирования будет устойчива, что также обозначено на рис. 18.12, а верт1шальной стрелкой.

Аналогичное заключение для области О /с /сгр можно сделать и в случае неустойчивого периодического решения на рис. 18.12, б, и в случае нал1гчия двух периодических решений на рис. 18.12, в, одно из которых устойчиво, другое неустойчиво. Если же автоколебания наблюдаются в области О А; ftrp, как показано на рис. 18.12, г, то естественно предположить, что область к > /сгр будет областью неустойчивости данной нел1шей-ной системы.

Наконец, если периодических решений для исследуемой нелинейной системы не получается вовсе ни при каких значениях ее параметров, tq согласно геометрическому способу определения автоколебаний (см. выше) получим, что кривая Михайлова будет либо охватьшать начало коордшат при всяком значении а, либо не охватывать его при всех а. Отсюда можно сделать вывод, что в первом случае данная нелинейная система устойчгша, а во втором - неустойчива.

Развитие, а также сравнение данного способа определения устойчивости равновесия нелинейной системы с методом Ляпунова, показьшающее эффективность такого способа, см. в книге [100], §§ 2.7-2.9.

§ 18.3. Примеры исследования нелинейных систем первого класса

Рассмотрим несколько примеров применения изложенного в предыдущ,ем параграфе метода.

Пример 1. Найдем влияние ограничения линейной характеристики двигателя (рис~. 18.13, а) на процессы в следящей системе. Пусть остальные

а) Мщ.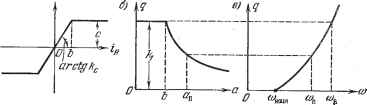

Рис. 18.13.

звенья системы линейны. Тогда уравнение управляемого объекта с двигателем вместо (16.63) примет вид

(ГоР + 1) рР = CF (g,

где F (in) определяется графиком рис. 18.13, а. Применяя к правой части этого уравнения формулы гармонической линеаризации (18.22) с заменой с = Ь/Сс, получаем уравнение управляемого объекта с двигателем в виде

. (ГоР + 1) рР = g {а) in, (18.65)

q = ki = ckc при а<;&.

g = -Ai(arcsinA + A/l ) при а>Ь,

(18.66)

что изображено графически на рис. 18.13, б. Здесь а обозначает амплитуду колебаний величины i .

Общее уравнение остальной части следящей системы согласно (16.53) будет

(Тр + 1) = - [й + (Тр + 1) кр] р. (18.67)

На основании (18.65) и (18.66) получаем характеристическое уравнение

(ГоР + 1) (ГвР + l)p + q{a){k + [Тр + 1) кр] = 0. (18.68)

После приведения его левой части к виду ар + ар + ар + з и подстановки р = /со получаем уравнения типа (18.36) в виде

X kq (йп) - [Го + Гв + Tksq (а] К = О, Y = {1 + Kq (йп)] СОп - ToTal = 0.

(18.69)

Выясним влияние параметра к (общего коэффициента усиления) на автоколебания в данной системе. Из последнего уравнения находим

8.70)

а из первого

Формула (18.70) дает график, изображенный на рис. 18.13, в, где

(18.71)

(18.72)

Графики на рис. 18.13, бив определяют связь между амплитудой и частотой сОд периодического решения в данной системе.

Найдем зависимость амплитуды Яц от величины параметра к. Для этого,

задаваясь разлнгчными сОд, будем брать из графтаа рис. 18.13 соответствующие значения а, а по формуле (18.71) вычислять к. В результате получим граф1ш п {Щ типа рис. 18.14, а или б. Чтобы определить, в каких случаях каждый из них 1шеет место, найдем /сщт-Дифференцируя (18.71) по СОп с учетом (18.70) и приравнивая результат нулю, получаем соответствующее значение со в виде

<-

Рис. 18.14.

(18.73)

причем /Сщт определяется подстановкой со в (18.70) и (18.71), а именно:

+ + (18.74)

Очевидно, что если со >- сов, то /сш iie существует и 1шеет место первый случай (рис. 18.14, а), а при сощ <; сое - второй (рис. 18.14, б). Сравнивая (18.73) и (18.72), приходим к выводу, что для системы, параметры которой удовлетворяют условию