нения. Поэтому из уравнения (18.48) или (18.51) сразу определяется амплитуда а затем из (18.49) или (18.52) - частота со д. Для систем с более сложными нелшгейностями получаются два уравнения с двумя неизвестными.

Учет временного запаздывания в нелинейной системе. В нелинейной системе, как и в линейной, может иметься постоянное по времени запаздывание т.

При этом уравнение линейной части (18.31) получит вид Q{p)Xi = -R (р) e-vx. Выражение (18.34) при этом будет

Q (/со) -\- R (/со) (cos тсо - / sin тсо) {q -\- jq) = 0. (18.53)

К уравнению (18.53) можно применить основной способ отыскания периодических репюний или другой из излонсенных выпю.

Устойчивость периодических решений. Выше уже указывалось, что не всякое периодическое решение уравнений собственного движения нелинейной системы будет соответствовать автоколебаниям, а только устойпшое. В конкретных задачах часто из физических соображений бывает сразу видно, возникают автоколебания или нет. Поэтому иногда нет нужды в математическом исследовании устойчивости найденного периодического решения. Однако в ряде случаев все же приходится этот вопрос исследовать.

Задача исследования устойчгшости периодического решения сводится, вообще говоря, к анализу линейного уравнения с периодическими переменными коэффициентами. А. М. Ляпуновым [82] разработаны соответствующие методы. Но их использование во многих случаях представляет пока еще большие трудности. Поэтому здесь строгое исследование устойчивости периодических решений излагаться не будет.

Опшпем три приближенных способа исследования устойчивости периодического решения: 1) осреднение коэффициентов, 2) использование кргшой Михайлова, 3) аналитический критерий.

Осреднение коэффициентов при исследовании устойчивости периодического решения. Запишем дифференциальное уравнение замкнутой системы в малых отклонениях Аж от исследуемого периодического решения: х - = йц sin cOni. Для линейной части системы на основании уравнения (18.31) получим

Q (р) Axi = - R (р) Ах. (18.54)

Уравнение нелинейного звена, например х = F (х, pxj), примет при этом для малых отклонений вид

-=(-)п-+(-)п- (18.55)

(аналогично и для других типов нелшейных уравнений), где индекс п означает, что в частные производные нужно подставить х = asin wt и рх = аоп cos сОп. Эти частные производные и являются периодическими-переменными коэффщиентами. В задачах теории регулирования ошг могут меняться как плавно, так и скачками (см. примеры в § 18.3). Осредним полученные периодические коэффщиенты, после чего вместо (18.55) будем иметь линейное уравнение с постоянными коэффициентами

Ажг = Ы ( п, Юп) + % ( ш Юн) р] A i, (18.56)

2я 2я

гр = п. (18.60)

Использование кривой Михайлова для исследования устойчивости периодического решения. Каждому конкретному значению а будет соответствовать определенная кривая Михайлова (18.45). При я = она пройдет через начало координат (рис. 18.9).

Для исследования устойчивости периодического решения с амплитудой а = п дадим малое приращение амплитуде Да. Тогда при я = и + Да кривая Михайлова займет либо положение 1, либо положение 2 (рис. 18.9). При этом, как известно из линейной теории (§ 6.3), кривая i, охватывающая начало координат, соответствует затухающим колеба-ПИЯМ переходного процесса, а Kpiman 2 - расходя-Щ1ШСЯ колебаниям.

Поэтому, если при Да > О Kpiman Михайлова займет положение i, а при Да <; О - положение 2, то переходный процесс в системе будет таким, что колебания с амплитудой, большей чем а, затухают, а коле-Рис. 18.9. бания с амплитудой, меньшей чем а, расходятся.

Следовательно, переходный процесс с обеих сторон сходится к исследуемому период1гческому процессу с амплитудой а- Это означает устойчивость последнего, т. е. в системе имеют место автоколебания. Если же при Да > О получится Kpiman 2, а при Да < О - кривая i, то переходный процесс в обе стороны расходится, т. е. исследуемое перио-д1гческое решение неустойчто (система устойчива в малом и неустойчива в большом, как на рис. 16.3, б).

Аналитический критерий устойчивости периодического решения. Развивая предыдущий способ, видим, что нет необходимости строить сами кривые Михайлова. Все исследование можно произвести аналитически. В самом деле, для того чтобы узнать, примет ли кривая Михайлова при Да > О положениеi (рис. 18.9), достаточно определить, куда будет перемещаться с увеличением а та точка кривой Михайлова (со = сОп), которая при а = находится в начале координат. Если она будет перемещаться по направлениям ОАг, ОА2 или OAg (рис. 18.10,а), то периодический процесс с амплитудой я ~ й устойчив, а если по направлениям ОА или ОА - неустойчив.

Это направление перемещения точки со = соц из начала координат с увеличением а определяется, очевидно, следующими проекциями на координатные оси X и F:

Характеристическое уравнение системы, определяющее устойчивость периодического решения, согласно (18.54) и (18.56) будет

Q{P) + R ip) Ы (й , СОп) + % (йп, п) р] = 0. (18.58)

Если оно удовлетворяет линейному критерию устойчивости, то исследуемое периодическое решение устойчиво.

В случаях, когда нелинейное звено описывается уравнением вида Х2 = - F (х (с гистерезисной петлей или без нее), осредненное характеристическое уравнение для исследования периодического решения будет

Q {Р) + R {р) {а = О, (18.59)

где Z и У обозначают вещественную и мнимую части аналитического выражения кривой Михайлова, а индекс п означает подстановку а = , со = = СОп. Как видно из рис. 18.10, я, для устойчивости исследуемого периодического решения вектор, определяемый проекциями (18.61), должен лежать с определенной стороны от касательной MN к кривой Михайлова, направление которой в свою очередь определяется проекциями

(Щ и (Щ .

(18.62)

Из расположения вектора с проекциями (18.61) по отношению к вектору с проекциями (18.62) и видна непосредственно устойчивость или неустойчивость данного периодического решения с амплитудой а.

На рис. 18.10, б 11 в показаны те же векторы, что и на рис. 18.10, а , но для других видов кривых Михайлова. Видно, что во всех случаях для устой-Ч1Ш0СТИ исследуемого периодического решения требуется, чтобы вектор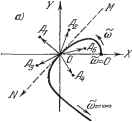

с3=0

Рис. 18.10.

С проекциями (18.61) лежал справа от касательной AfiV, если смотреть вдоль кривой Михайлова в сторону возрастания со, причем направление касательной MN определяется вектором с проекциями (18.62). Это геометрическое условие устойчивости периодотеского решения можно записать в следующем аналитическом виде:

или иначе:

/ дХ дд

дХ дд

дд да дд да

) (Щ ~(Щ (

In \ да) l-a \ да) /пА

dY дд dY дд дд да дд да

0.

Здесь важно, что частные производные берутся не по частоте со, а по текущему параметру кривой Михайлова со, т. е. имеются в виду выражения X и Y не в форме (18.35), а как вещественная и мнимая части выражения (18.45) в функции от со при со = const (если она входит в коэффщиенты, стоящие в квадратных скобках этого выражения).

Выполнение условия (18.63) устойчивости периодического решения во всякой конкретной задаче можно проверить аналитически, без построе-Ш1Я кривьо:. Этого достаточно для систем третьего и четвертого порядков, если все коэффициенты гармонически линеаризованного характеристического уравнения положительны. Для систем же пятого и более высокого порядков требуется дополнительно проверить общий ход кртой Михайлова, чтобы убедиться, что имеет место случай, например, рис. 18.11, а, но не рис. 18.11, б. Замет1ш, что вместо построения кривой Михайлова можно и тут воспользоваться аналитическим дополнительным условием, потребовав