Зададимся различными числовыми значениями амплитуды аш получим для каждого из них по уравнениям (18.38) зависимости

к = к{ап) шТ = Т {а>.

После этого, меняя соц, можно построить по точкам соответствующие кривые и = const в координатах {к, Т), как показано сплошными линиями на

рис. 18.5, е. На этих кривых получаются отметки частот © , которые также можно соединить (пунктирные кривые).

График рис. 18.5, е позволяет выбирать значения двух параметров {к ж Т) нелинейной системы. Если такие графики построить для различных возможных структурных схем системы, то можно будет выбирать также и наивыгоднейшую структурную схему проектируемой замкнутой автоматической системы с учетом нелинейностей.

Использование графиков коэффициентов гармонической линеаризации. Во многих задачах коэффициенты д ж д, входящие в уравнение (18.34), сложно зависят от амплитуды а, а Б ряде случаев и от частоты ю. В таких случаях удобнее указанное уравнение записывать в виде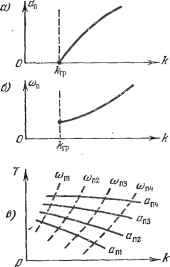

Рис. 18.5.

Q (у ) + R (/со) ig + jq) =-- О, (18.39)

не подставляя зависимости д ж д от: а ж а. Тогда вместо уравнений (18.36) получим для определения периодического решения уравнения:

X (со, д, д) = О, У (со, д, д) = 0. (18.40)

Для общего случая задач, в которых каждый из коэс)фициентов гармонической линеаризации q ж д зависит сложным образом от обеих неизвестных а и со, т. е.

д = gia, со), q = д (й, со), (18.41)

можно применить следующий прием решения.

Задаваясь различными значениями а и со, построим по формулам (18.41) две серии кривых: q (со) и д (со) при разных а = const (рис. 18.6). Затем из уравнений (18.40) выразим

д = Zi (со), д = (со)

(18.42)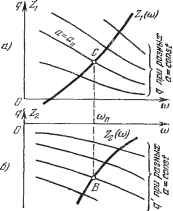

н эти две кривые нанесем на тех же графиках. Теперь остается на этих двух кривых найти такие точки С ж В, в которых кривые Z (со) ы Z (со) пересекают линии с одинаковыми зиа-чениями а при одном и том же значении со. Получепные величшш й и со будут решением задачи, т. е. амплитудой ж частотой сОт, искомого шения.

Во многих встречающихся на практике задачах вместо (18.41) будет

Рис. 18.G.

периодического ре-

Тогда кривые q и q на рис. 18.6 для разных амплитуд будут шиеть вид горизонтальных прямых линий.

В простейшем случае, когда в системе имеется однозначная нечетно-симметричная нелинейность F (ж), для которой q - q{a) ш q = О, из уравнений (18.40) можно найти

q{a)=Z (to). (18.44)

Тогда, исключив q из уравнений (18.40), найдем частоту со = соц как функцию параметров системы. Затем, изобразив график зависимости q (я) (рис. 18.7), проведем на нем согласно (18.44) горизонтальные линии q - Z (со) для разных постоянных значений со=сОп, т. е. для разных соотношений параметров системы. Точки пересечения этих прямых (со = СОп) с кривой q {а) (например, на рис. 18.7 точки п! и йпг) определяют в каждом случае амплитуды периодических решений. Если пересечений нет, то и периодических решений в системе не будет. В простейших случаях уравнение (18.44) решается аналитически.

Графический способ. Для гармонически лшеаризованного характеристического уравнения (18.33) можно написать выражение кривой Михайлова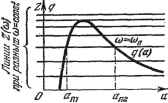

Рис. 18.7.

Dm=Q(0) + E{j) q{a, со)

g (Д, со) со

(18.45)

где знак ~ введен, чтобы отличать текущий параметр со, изменяющийся вдоль кривой Михайлова, от частоты со, входящей в выражение гармонической линеаризации нелинейности.

Тогда при любых заданных постоянных а и со кривая Михайлова будет иметь такой же вид, как для обыкновенных линейных систем. Искомое периодическое решение = sin сОп*, т. е. неизвестные и со, определятся прохождением кривой Михайлова через начало координат (рис. 18.8, а).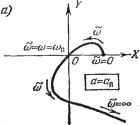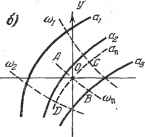

Рис. 18.8.

Поскольку в точке прохождения кривой Михайлова через начало координат текущее значение со должно совпадать со значением со = сОд, входящим в коэффициенты гармонической линеаризации, то для удобства решения можно заранее отождествить в выражении (18.45) значения со и со. Тогда искомые частоту со - соп и амплитуду й = автоколебаний можно будет определить путем построения кривых

/ (со) = (? (/со) -\- R (/со) [q {а, со) -\- jq {а, со)], (18.46)

которые в общем случае не будут совпадать с кривыми Михайлова. При этом надо выбрать такое значение а, при котором кривая пройдет через начало координат.

Если например, для каких-нибудь трех различных значений а кривые / (со) проходят указанным на рис. 18.8, б образом, то искомые значения a = jjH со = сОд можно найти путем следующей интерполяции:

ап = Й2 + (аз -Яг). п = 1( 2 - i)-

Этот способ целесообразен лишь в самых сложных случаях, когда изложенные выше способы не удается применить.

Использование коэффициентных соотношений для определения периодического решения. Для обнаружения факта наличия пары чисто мнтых корней в характеристическом уравнении (18.33) можно также применить известные алгебраические критерии устойчивости лшаейных систем. Так, если гармонически линеаризованное уравнение (18.33) нелинейной системы имеет третью степень относительно р, то его можно записать в виде

аоР + (hP + аР + йз = О, (18.47)

причем коэффициенты его будут содержать в себе искомые значения частоты со и и амплитуды автоколебаний.

Условие наличия пары чисто мнимых корней по критерию Гурвица (см. § 6.2) будет

= о з> (18.48)

оно дает только одно уравнение с двумя неизвестными и сОп- Чтобы найти второе, представим уравнение (18.47) при наличии мнимых корней р = = + /СОп в виде

{р + coS) (йоР + Ь) = 0.

Раскрьш здесь скобки и приравняв коэффициенты этого уравнения соответствующим коэффициентам (18.47), найдем

йоСо = а. (18.49)

Из двух уравнений (18.48) и (18.49) определяются неизвестные амплитуда йп и частота сОп автоколебаний, входящие в состав коэффициентов (18.47). При этом точно так же, как в основном способе, здесь на основании уравнений (18.48) и (18.49) можно строить графики завис1шостей йд и сОд от одного параметра системы или на плоскости двух параметров с целью их выбора.

Если гармонически линеаризованное уравнение (18.33) нелинейной системы имеет четвертую степень относительно р:

ар -г -\- Й2Р + ар + Й4 = О, (18.50)

то условие нал1гчия пары чисто мнимых корней согласно § 6.2 будет

йз ( % 2 - Оз) - 41 = О- (18.51)

Кроме TorOi записывая уравнение (18.50) в виде

(р + К) {аоР + hp + 62) = О,

раскрывая здесь скобки и приравнивая полученные коэффициенты соответствующим коэффициентам (18.50), находим

йсо = ад. (18.52)

С помощью двух уравнений (18.51) и (18.52) решаются все вьшгеуказан-ные задачи для нелинейной системы четвертого порядка.

Заметим, что для систем с нелинейностью вида = F (ж) без гистерезисной петли частота со не входит в коэффициенты характеристического урав-