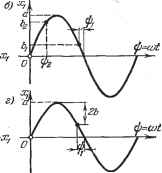
(18.15)

а уравнение релейного звена с характеристикой вида рис. 18.1, а будет иметь вид (18.9) с полученными здесь значениями q (а) и q (а). Рассмотрим частные случаи.

Для релейного звена с характеристикой без гистерезисной петли, но с зоной нечувствительности b (рис. 18.1, г), полагая m = 1, из вышенаписан-ных формул получаем

д = со8ф = -]/1-, ? = 0 (а>Ь). (18.16)

Для релейной характеристики с гистерезисной петлей типа рис. 18.1, д, полагая т = - 1, имеем

д = £-со8ф1 = -т/ 1 - па па Г

(18.17)

Наконец, для идеального релейного звена (рис. 18.1, е), полагая 6 = 0, находим

= = 0. (18.18)

На последнем примере легко видеть смысл гармонической линеаризации релейной характеристики. Написанное выражение для q означает замену ломаной характеристики ABCD прямолинейной MN (рис. 18.1, е) с таким наклоном, чтобы эта прямая MN приблизительно заменяла собой тот участок ломаной ABCD, который охватывается заданной амплитудой а. Отсюда становится вполне понятной обратно пропорциональная зависимость q от а, даваемая формулой (18.18), так как чем больше амплитуда а колебаний входной величины х, тем более пологой должна быть прямая MN, приблизительно заменяющ;ая ломаную ABCD.

Аналогично обстоит дело и с релейной характеристикой на рис. 18.1, г, для которой наклон заменяющей ее прямой дается формулой (18.16). Следовательно, всякое безгистерезисное релейное звено в колебательном процессе эквивалентно такому линейному звену, передаточное число (коэффициент усиления) которого q (а) уменьшается с увеличением амплитуды колебаний входной величины, начиная с а - fe /2.

Что касается релейного звена с гистерезисной петлей, то согласно (18.9) и (18.17) оно заменяется линейным звеном с аналогичным прежнему козффи-

Следовательно, после использования свойств (18.12) каждый из интегралов (18.10) разбивается на три слагаемых:

я ;Ф2 я

причем первое и третье из них согласно рис. 18.1, й и б будут нулями. Поэтому выражения (18.10) принимают вид

ф! Фг

ф2 Ф1

откуда

= li( *- 2)=(/ 1- + ]/ 1--

циентом усиления q (й), но кроме того, еще с введением отрицательной производной в правой части уравнения. Введение отрицательной производной в противовес положительной (см. § 10.2) вносит отставание по фазе в реакции звена на входное воздействие. Это служит линейным эквивалентом , заменяющим эффект действия нелинейности в виде гистерезисной петли. При этом коэффициент q {а) при производной согласно (18.17) тоже уменьшается с увеличением амплитуды а колебаний входной величины х, что и понятно, так как эффект влияния гистерезисной петли на процесс колебаний в релейном звене должен быть тем меньше, чем больше амплитуда колебаний по сравнению с шириной гистерезисной петли.

Коэффициенты гармонической Л1шеаризации других простейших нелинейных звеньев. Рассмотрим нелинейное звено с зоной нечувствительности и с насьнцением (рис. 18.2, а). Согласно рис. 18.2, б, где

ф} = arcsin

4p2 = arcsin = arcsin

с-\-Ъф ак

(18.19)

интеграл (18.10) на участке (О, л) разбивается на пять слагаемых, причем два из них равны нулю. Поэтому

Фа -*2

q=- \ A;(asinx!) - bj) sin xj) -)--\ csinipdt])-]-

j (a sin ij) - fej) sin dxj).

откуда с заменой с = (&2 - к ж = а sin щ, = а sin получаем

g = (il2-!)i-h4-sin2il)2-ysin2x!)i) {a->h), (18.20)

где и-фа определяются формулами (18.19). Ввиду отсутствия гистерезисной петли здесь q = 0.

Итак, уравнение нелинейного звена с характеристикой вида рис. 18.2, а будет х = q (а) х, где q (а) определяется выражением (18.20).

arctgk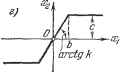

Рис. 18.2.

Как частный случай отсюда получается значение q {а) для звена с зоной нечувствительности без насыщения (рис. 18.2, в). Для этого в предыдущем

решении нужно положить а < fe и, следовательно, Фг = -g да

Как ВИДИМ, звено с зоной нечувствительности уподобляется здесь линейному звену с уменьшенпьпи за ее счет коэффициентом усиления. Это уменьшение коэффициента усиления значительно при малых амплитудах и невелико при больпшх, причем О q (а) при fe а оо.

Для второго частного случая - звено с насьщением без зоны нечувствительности (рис. 18.2, г), - полагая = О, т. е. ф = О, из (18.20) и (18.19)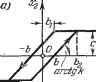

получаем

arcsin

(18.22)

(°>т).

причем при а имеем q =

= к (линейная характеристика). При амплитудах колебания входной величины, захватывающ;их зону насы-ш,ения, данное звено заменяется как бы линейным звеном с тем меньшим коэффициентом усиления q (а), чем больше амплитуда (в противоположность предыдущему).

Для звена с переменным коэффициентом усиления согласно рис. 18.2, д и е по формуле (18.10) с учетом (18.12) получаем

Рис. 18.3.

q = j ка sin ф sin ф йф -f

-f- j [/(;2(йsiпф -fo)-b/(;ife] siпфdф-f что с заменой sin Ф1 = fe дает

j ка sin ф sin ф йф.

qk2-~{K~K) (arcsin--fl/l --g-) (a>fe). (18.23)

Здесь ломаная характеристика (рис. 18.2, 8) заменяется одной прямой со средним между к и к наклоном q (а), причем этот наклон изменяется в интервале кд (а) feg при увеличении амплитуды fe а оо. Для амплитуд а <аЬ имеем линейную характеристику с наклоном к-.

Для нелинейного звена с насыщением и с гистерезисной петлей (рис. 18.3, а) уравнение получит уже вид (18.9), где согласно рис. 18.3, б и формулам (18.10)

% л-*!

g j/c(asiпф-fe) siпфdф-}-- j csinфdф--

j Л (a sin Ф-f fe) sin Ф йф;

Л-фJ