0 2л

q = -- I F {a sin ф, со cos ф) cos ij) dij;.

(18.7)

Итак, нелинейное выражение (18.1) при ж = а sin cof заменяется выражением (18.6), которое с точностью до высших гармоник аналогично линейному. Эта операция и называется гармонической линеаризацией. Коэффициенты q (а, со) и q {а, со) постоянны при постоянных значениях й и со, т. е. в случае периодического процесса. В переходном колебательном процессе с изменением а и со коэффициенты qwi q изменяются (см. гл. 20). Для разных амплитуд и частот периодических процессов коэффициенты выражения (18.6) будут различны по величине. Это очень важное для дальнейшего обстоятельство является существенным отличием гармонической лкшеаризации, но сравнению с обьганьш способом лкшеаризации (§ 3.1), приводящим к чисто Л1шейным выражениям, которые применялись в предыдущих разделах книги. Указанное обстоятельство и позволит путем применения к выражению (18.6) линейных методов исследования проанализировать основные свойства нелЕшейных систем, которые не могут быть обнаружены при обьганой линеаризации.

Приведем также формулы гармонической линеаризации для более простой нелЕшейности:

y = F{x). (18.8)

Здесь возможны два варианта: 1) кривая F (х) имеет гистерезисную петлю (например, рис. 16.18, в, рис. 16.22, г, д), и 2) кривая F {х) не имеет гистерезисной петли (рис. 16.8, б, рис. 16.22, а и др.)..

При наличии гистерезисной петли,- когда фактически наблюдается зависимость от знака производной, нелинейная функция у = F (х) после гармонической линеаризации заменяется следующим выражением (при ж = й sin со:

q{a) р х-высшие гармоники, . (18.9)

2л 2л

ЧТО означает отсутствие постоянной составляющей в данном разложении. В настоящей главе будет везде предполагаться выполнение условия отсутствия постоянной составляющей (18.5). Впоследствии (глава 19) будет дан метод исследования автоколебаний при наличии постоянной составляющей, т. е. в случае невыполнения условия (18.5).

Если принять во внимание, что из (18.2) и (18.3)

Sin ф = - и cos ll) = а ею

то формулу (18.4) при условии (18.5) можно будет записать в виде

y = q{a,(ii)x-\- рх-\-высшие гармоники, , (18.6)

где q ж q - коэффициенты гармонической линеаризации, определяемые формулами:

jjP(asini];, ococosi])) sinipdi];.

при условии отсутствия постоянной составляющей:

F(asinTl))dtl) = 0.

Если же кривая F (х) не имеет гистерезисной петли, то = О, так как при а: = а sin -ф будет

2я о

(при гистерезисной петле этот интеграл не был нулем вследствие различия в очертании кривой F (х) при возрастании и убывании х).

Следовательно, при отсутствии гистерезисной петли нелинейное выражение (18.8) заменяется более простьш-

у = д (а) X -\- высшие гармоники,

т. е. криволинейная или ломаная характеристика у = ЕЦх) с точностью до высших гармоник заменяется прямолинейной, тангенс угла наклона которой q зависит от размера амплитуды колебаний а. Другими словами, нелинейное звено уподобляется линейному с передаточным числом (коэффициентом усиления), зависящим от амплитуды а колебаний входной величины х.

Гистерезисная же петля вводит согласно (18.9), кроме того, еще производную, дающую отставание по фазе, так как q (а) < 0. Таким образом, нелинейное отставание по координате в виде гистерезисной петли превращается при гармонической линеаризации в эквивалентное линейное отставание по фазе.

Можно создать специальное нелинейное звено с опережающей петлей, что будет эквивалентно линейному опережению фазы при введении производной, но с тем отличием, что величина опережения фазы будет зависеть от размера амплитуды колебаний, чего нет в линейных системах.

В случаях, когда нелинейное звено описывается сложным уравнением, включающим сумму различных линейных и нелинейных выражений, каждый из нелинейных членов подвергается гармонической линеаризации по отдельности. Произведение же нелинейностей рассматривается обязательно в целом как одна сложная нелинейность. При этом могут встретиться иного характера нелинейные функции.

Например, при гармонической линеаризации второго из уравнений (16.3) придется иметь дело с функцией F {рх, рх) при х = а sin at. В этом случае получаем

F{pX, рх) =

х-\-шсшие гармоники,

2 = - j F (-а(о2 81пф, асосоеф) 81пфйф,

при условии

F (~ag)sin\j3, аюcosф) cosфйф

j F (--acosin ag)cosф) йф = 0.

(18.11)

Если же функция F {рх, рх) или функция F {рх) будет единственной нелинейной функцией в уравнении нелинейного звена, то при гармонической

линеаризации можно положить рх = а sin (at ш

F (рх, рх) = д{а,(а) рх-{- рх+высшие гармоники

аналогично прежним формулам (18.6 и (18.7). Но при этом величина а во всех выкладках будет амплитудой колебаний скорости рх, а не самой координаты X. Последняя же будет иметь тогда амплитуду а = о/со.

При вычислении коэффициентов гармонической линеаризации по формулам (18.10) надо иметь в виду, что при симметричных нелинейных характеристиках интеграл (О, 2я) можно получить удвоением интеграла (О, л), т. е.

2л л

(18.12)

а для симметричных относительно начала координат безгистерезисных характеристик F {х) при вычислении д (а) можно писать

2л л/2

(18.13)

Приведем выражения для коэффициентов некоторых простейших нелинейных звеньев. Затем их можно будет непосредственно использовать при решении различных конкретных задач.

Коэффициенты гармонической линеаризации релейных звеньев. Найдем коэффициенты q {а) и q (а) уравнений наиболее типичных релейных звеньев по формулам (18.10). Возьмем общий вид характеристики релейного .звена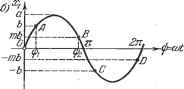

д) т=-1

*Ь с 1

Рис. 18.1.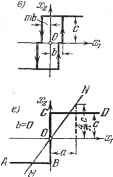

х = F (i), изображаемой графиком рис. 18.1, а, где т есть любое дробное число в интервале - 1 m 1. Как частные случаи будут получены уравнения других типов релейных звеньев.

Если колебания входной величины х = а sin cof имеют амплитуду а<Ъ, то согласно рис. 18.1, а движения в системе не будет. Если амплитуда а> Ь, то переключения реле происходят в точках А, В, С, D (рис. 18.1, б),в которых имеем