В системах с переменной структурой следует стремиться реализовать скользящий режим. Для этого переключения в системе должны производиться в таких местах, где фазовые траектории направлены навстречу друг другу. Покажем это па примере.

Пусть в той же системе (рис. 17.22) звено также устроено по принципу рис. 16.27, а, по

xi=--y - cx, где у.

(П.127)

Тогда прежнее выражение для W:

при при

XiX>0,

xix<:o,

получает другой смысл. Возьмем при этом

а = ki, Р = - к.

Получим два уравнения системы:

-\-kikx=0 при XiX>0,

dt dx

- kikx - О при XiX < 0.

(17.128) (17.129)

Линиями раздела между областями их действия будут

X = О и Xl == у - СХ = О,

т. е. ось ординат и наклонная прямая на фазовой плоскости (рис. 17.24). При этом уравнение (17.128) будет действовать в первом и третьем секторах фазовой плоскости. Поэтому там фазовыми траекториями будут служить согласно рис. 16.8 концентрические эллипсы. Уравнение же (17.129) будет действовать во втором и четвертом секторах фазовой плоскости (рис. 17.24), где фазовые траектории изобразятся в соответствии с рис. 16.3.

Обе эти линейные структуры (17.128) и (17.129) по отдельности не обладают устойчивостью. Благодаря же переключениям система в целом становится устойчивой.

В отличие от предыдущей системы, здесь, как видно из рис. 17.24, нет колебательного процесса. При любых начальных условиях фазовая траектория прихо-паклонную прямую х- = О, где она встречается с фазовой траек-с противоположным ей направлением движения. Поэтому пере-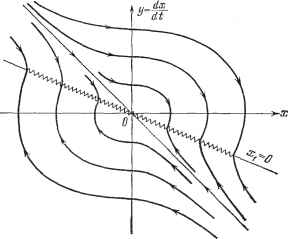

Рис. 17.24.

дит па торией

ход изображающей точки через прямую Xi = О невозможен. В результате изображающая точка вынуждена двигаться вдоль прямой = О в сторону начала координат, что и представляет собой скользящий режим переходного процесса в данной системе.

§ 17.51 ИССЛЕДОВАНИЕ СИСТЕМ С ПЕРЕМЕННОЙ СТРУКТУРО]2 539

Практически скользящее движение будет сопровождаться вибрациями вследствие быстрых переключений то в одну, то в другую сторону, как и показано на рис. 17.24. Ввиду неидеальпости системы (дополнительной инерционности или запаздывания) эти вибрации будут иметь конечные амплитуду и частоту. При идеальном же рассмотрении, проведенном выше, амплитуда их равна пулю, а частота - бесконечности.

Рассмотрение реального переходного процесса скользящего типа с конечными вибрациями за счет дополнительной инерционности, повышающей порядок уравнения, возможно с помощью приближенного метода гармонической линеаризации. Это можно сделать аналогично рассмотрению медленно меняющихся сигналов в автоколебательных системах (§ 19.2), если за медленно меняющийся сигнал принять основное апериодическое движение в скользящем процессе, а наложенные па него вибрации рассчитать, как автоколебательную составляющую процесса (см. [101]).

ГЛАВА 18 .

ПРИБЛИЖЕННЫЕ МЕТОДЫ ИССЛЕДОВАНИЯ УСТОЙЧИВОСТИ И АВТОКОЛЕБАНИЙ

§ 18.1 Гармоническая линеаризация нелинейностей

В этой главе будет изложен метод гармонической линеаризации для приближенного определения периодических решений (автоколебаний) и устойчивости нелинейных систем любого порядка, который по идее близок к методу эквивалентной линеаризации или методу гармонического баланса Н. М. Крылова и Н. Н. Боголюбова, а по результатам - также и к методу малого параметра Б. В. Булгакова.

Рассматриваемый приближенный метод является мощным средством исследования нелинейных автоматических систем в смысле простоты и довольно большой универсальности его аппарата в применении к самым разнообразным нелинейностям. Однако надо иметь в виду, что он решает задачу приближенно. Имеются определенные ограничения его применимости, о которых будет сказано ниже. Эти ограничения обычно хорошо соблюдаются в задачах теории автоматического регулирования. Практические расчеты и эксперимент показывают приемлемость этого метода для многих видов нелинейных систем.

Пусть дано какое-нибудь нелинейное выражение вида

у = F{x, рх) (18.1)

и задано

ж = а sin ф, ф = tui!. (18.2)

Тогда

рх = ati) cos ф. (18.3)

Разложив функцию в правой части выражения (18.1) в ряд Фурье, получим

У = -

j F (а sin ф, ati) cos ф) йф --

-f jF(asinф, a(вcosф)sinфdф sinф--

F(asinф, сив cos ф) cos ф <ф cosвысшие гармоники. (18.4)

Положим

j F (а sin ф, ati) cos ф) йф = О, (18.5)