§ 17.4]

ЧАСТОТНЫЙ МЕТОД В. М. ПОПОВА

теорема не выполняется, т. е. нелинейная система не имеет абсолютной устойчивости.

Заметим, что, например, в задаче о самолете с автопилотом (§ 17.2) условие (17.54) означает любое расположение нелинейной характеристики во всем первом (и-третьем) квадранте. Во всех подобных случаях согласно

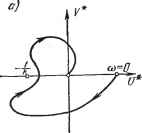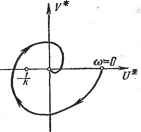Рис. 17.19.

Рис. 17.20.

рис. 17.17 имеем /с = оо. В теореме В. М. Попова при этом вместо (17.116) получаем условие

Ве (1 + iti>h) W (щ) > О, (17.120)

а вместо (17.118)

и* ((0) ~ hoV* ((о) > О (17.121)

при всех (О > 0. Поэтому в графической интерпретации прямая должна проходить не так, как показано было на рис. 17.19, а через начало координат.

В частности, для указанного примера (§ 17.2) уравнения (17.63) можно преобразовать к виду

У= f {xg), (1 + Р) Pxg = [rp + (1 + г) р -f т] J/.

где обозначено у = - рх, причем р - производная по т. Передаточная функция линейной части системы будет

W{p)

rpg-K14-r)p4-Y

(1+р)р2

Отсюда

W (/(О)

-rc3g-h/(l+r)c3-fY

-СЭМ1+/СЭ)

умножив числитель и знаменатель на 1 - /со, получим

-ReW (Ш=- ImTFfto) (l+r-y) ю+гсрз

а согласно (17.117)

- ю2(1+(02)

Неравенство (17.121) принимает вид

- 1 -с02

- (у + а) + ho {1 + Г - у + га) > 0.

(17.122)

(17.123)

Очевидно, что это неравенство может быть выполнено при любом со > О,

если

[1 + г - 7 > О (17.124)

и если h берется сколь угодно большим, чтобы обеспечить неравенство (17.123) при сколь угодно малых со.

. Полученное условие (17.124) выполняется при

г > 7 - 1, если 7 > 1, г > О, если О < 7 < 1,

что точно совпадает с найденными ранее условиями абсолютной устойчивости данной системы (17.69) и (17.70). Смысл практической реализации этих условий был разъяснен в § 17.2.

Графически критерий устойчивости выражается в том, что вся кривая W* (/(о) = и* ((b) 4- ]V* ((b), построенная согласно (17.122), расположена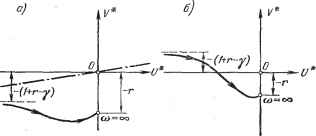

Рис. 17.21.

(рис. 17.21, а) справа от прямой U* - hV* - О, обозначенной штрих-пунктиром, со сколь угодно малым наклоном, если 1 -Ь г - 7 > 0. Если же 1 4-+ г - 7 < О (рис. 17.21, б), то такую прямую провести невозможно и, следовательно, нелинейная система не будет абсолютно устойчивой.

Здесь был приведен простой пример, в котором условия устойчивости по методу В. М. Попова выражаются в общем буквенном виде. В большинстве технических задач этого не получится. Однако видно, что описанный частотный критерий устойчивости В. М. Попова для систем с одной однозначной нелинейностью в его графической форме может быть применен при любой сложности линейной части системы и численно заданных коэффициентах уравнений. Более того, он может быть применен в случае, когда не заданы уравнения, но известна экспериментально снятая амплитудно-фазовая частотная характеристика линейной части Wijti)). Чтобы установить устойчивость системы согласно рис. 17.19, W (/(в) надо перестроить в характеристику W* (jco), по-льзуясь формулами (17,117).

§ 17.5]

ЕЕИССЛЕДОВАНИЕ CHCTEMSCgnEPEMEHHOaiCTPyKTyPOSiJ

Очертание нелинейности может быть неизвестным. Необходимо знать лишь, в пределах какого угла (рис. 17.17) она расположена. Для конкретно заданных форм нелинейности область устойчивости, вообще говоря, будет несколько шире, но данным методом это не определяется (см. главу 18).

§ 17.5. Исследование систем с переменной структурой

Понятие о системах с переменной структурой было дано в начале книги (§ 2.3), а об их уравнениях - в конце главы 16.

Покажем методику исследования систем с переменной структурой при отсутствии внешнего воздействия на примере системы второго порядка при линейном объекте и линейных структурах регулятора, так что нелинейность системы будет заключаться в автоматическом переключении этих структур.

Имея в виду второй порядок системы, используем изображение процессов на фазовой плоскости, которое для линейных систем представлено было выше на рис. 16.8-16.13.

Рассмотрим систему (рис. 17.22), не обладающую при постоянной структуре

Рис. 17.22.

Рис. 17.23.

собственной устойчивостью [42]. В самом деле, если ¥ = const, то уравнение системы будет

и получатся незатухающие колебания, изображаемые на .фазовой плоскости концентрическими эллипсами (рис. 16.8).

Если же звену ¥ придать вид, как на рис. 16.27, а, где х- =-jt- с пере-

ключением согласно формуле (16.71), где а = /с, р = Ag, причем ki>k2> О, то получим зфавнения системы

kikx = 0 при xix>0, (17.125)

-Ь kzkx = О при XiX<C 0.

(17.126)

Первое из них будет действовать в первом и третьем квадрантах фазовой плоскости (рис. 17.23), а второе - в четвертом и втором квадрантах. С эллипса 7 в первом квадранте (соответствует коэффициенту /с) изображающая точка переходит на эллипс 2 в четвертом квадранте (соответствует коэффициенту Аг), затем на эллипс 3, концентрический с первым (снова коэффициент к), далее на эллипс 4, концентрический с эллипсом 2, и т. д. В результате таких переключений система становится устойчивой.

В данном примере переходный процесс представляет собой затухающие колебания. В большинстве случаев для избежания колебательных процессов