Для вычисления амплитуды автоколебаний нужно сначала по формулам (17.96) записать решения для и о, а именно:

г, = с7,Л---е~М,

+к,п (1--Ч: yt (Г- .).

Затем по последней из формул (17.104) надо записать решение для угла рыскания самолета ф {t) и угла отклонения руля = г, что дает

==ckiT

{T-t) + t-

= c(t-~) (0<f<r).

(17.112)

По этим уравнениям можно построить графики автоколебаний самолета (рис. 17.16, б) и руля (рис. 17.16, е), причем

- fcp+i / 2

Амплитуда автоколебаний руля, как видно из рис. 17.16, в, будет

где с - скорость движения руля согласно характеристике рис. 17.15.

Амплитуда автоколебаний самолета (по углу рыскания) Яф найдется как максимум функции ф (f) на участке О <Z t <Z Т. Взяв от ф (17.112) производную по f и приравняв ее нулю, получаем следующее уравнение для определения времени t = t, соответствующего максимуму ф:

2{kp + Ti)

Л~-тр- = те 2-1, где т =

Это уравнение решается графически, как показано на рис. 17.16, г. Определив таким образом величину t, подставляем ее в первую из формул (17.112), что и дает искомую амплитуду автоколебаний самолета

Яф = Ф (*м)-

Частота же автоколебаний определяется через полупериод Г, найденный на основании уравнения (17.105) .графически (рис. 17.16, а).

Заметим, что задача в данном примере ради простоты решена лишь для упрощенного уравнения движения самолета по курсу (первое из уравнений (17.101)) и в предположении строгого постоянства скорости рулевой машинки.

§ 17.43 Частотный метод В. М. Попова

Решение задачи об абсолютной устойчивости системы с одной однозначной нелинейностью (т. е. устойчивости при любой форме этой нелинейности со слабым ограничением типа (17.54) или типа рис. 17.14) с помощью теорем прямого метода Ляпунова было проиллюстрировано па двух примерах в § 17.2.

Изложим теперь частотный метод, предложенный румынским ученым В. М. Поповым [97], при использовании которого та же задача решается более просто приемами, аналогичными частотным способам исследования устойчивости линейных систем.

Если в системе автоматического регулирования имеется лишь одна однозначная нелинейность

У =F (ж).

(17.113)

то, объединив вместе все остальные (линейные) уравнения системы, можно всегда получить общее уравнение линейной части системы (рис. 17.17, а) в виде

Q{p)x = -R {р) у,

(17.114)

Линейная часть

- Нелинейность -I

Q(j>) = аор + ар- 4- . . . + a -iP + Оп,

причем будем считать т <С п

Пусть нелинейность у = F (х) имеет любое очертание, не выходящее за пределы заданного угла arctg к (рис. 17.17, б), т. е. при любом X

OFixXkx. (17.115)

±1усть многочлен Q (р) или, что то же, характеристическое уравнение линейной части Q (р) = О имеет все корни с отрицательными вещественными частями или же кроме них имеется еще не более двух нулевых корней. Другими словами, допускается, чтобы an = О или а = О и = О в выражении Q {р), т. е. не более двух нулевых полюсов в передаточной функции линейной части системы

Приведем без доказательства формулировку теоремы В. М. Попова: для установления устойчивости нелинейной системы достаточно подобрать такое конечное действительное число h, при котором при всех со О

Рис. 17.17.

Re(l-b/o))PF(jo))-b>0,

(17.116)

где W (/(о) - амплитудно-фазовая частотная характеристика линейной части системы. При наличии одного нулевого полюса требуется еще, чтобы

Im W (/(0)

оо при (0-0,

а при двух нулевых полюсах Re W (/(о) -> - оо при (О

О, а Im (/(о) < О при малых со.

и* ((0) = Re (7(0) = ReW Ца>),

V* ((о) = 1ш W* (/(о) = (оГо Im W(]a),

(17.117)

где = 1 сек - нормирующий множитель.

График W* Ою) имеет вид (рис. 17.18, а), аналогичный W (jto), когда в выражениях Q {р) ж R {р) разность степеней п - те > 1. Если же разность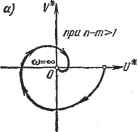

Рис. 17.18.

степеней п - т ~ \, чо конец графика будет на мнимой оси ниже

начала координат (рис. 17.18, б).

Преобразуем левую часть неравенства (17.116):

Re (1 + ]Щ W (/(О) + = Re PF (/to) -mhlmW(/со)---i. Тогда, положив

W* (/со) = и* (со) + /F* (со)

и использовав соотношения (17.117), получим вместо (17.116) для теоремы Б. М. Попова условие

и* (О)) -У ( ) + (со)-hoV* (со)-f 1 >О

при всех (О 0.

Очевидно, что равенство

г7*(со)-оУ* H+Y =

(17.118)

(17.119)

представляет уравнение прямой на плоскости W* (/со).

Отсюда вытекает следующая графическая интерпретация теоремы В. М. Попова: для установления устойчивости нелинейной системы достаточно подобрать такую прямую на плоскости TF* (/со), проходящую через точку

I - ~, /OJ , чтобы вся кривая W* (/со) лежала справа от этой прямой.

На рис. 17.19 показаны случаи выполнения теоремы. В этих случаях нелинейная система устойчива при любой форме однозначной нелинейности, ограниченной лишь условием (17.115). На рис. 17.20 показаны случаи, когда

Теорема справедлива также и при наличии в знаменателе Q (р) передаточной функции линейной части не более двух чисто мнимых корней, по при этом требуются некоторые другие простые добавочные условия [2], называемые условиями предельной устойчивости.

Другая формулировка той же теоремы, дающая удобную графическую интерпретацию, связана с введением видоизмененной частотной характеристики W* (/< ), которая определяется следующим образом: