Пример. Рассмотрим систему самолета с курсовым автопилотом (в упрощенном виде), которая исследовалась в § 17.2, но только характеристику привода руля возьмем релейную в виде рис. 17.15. В § 17.2 были получены условия устойчивости системы на основании теорем Ляпунова (устойчивость системы по отношению к устаноышшемуся состоянию с постоянным значением угла курса). Теперь же будем искать автоколебания и условия, при которых они имеют место.

Уравнения самолета и автопилота согласно (17.55), (17.60) и (17.59) запишем здесь в виде

pl = F{o),

(17.101)

где ijj - отклонение самолета от заданного курса, § - отклонение руля, о - управляющее воздействие на рулевую машинку (в закон регулирования введена производная и имеется обратная связь). Пусть последнее из уравнений (17.101) изображается графиком рис. 17.15 (рулевая машинка постоянной скорости).

Положив

рф = Xi, ijj = х, (17.102)

приведем уравнения (17.101) к виду (17.81). В наших обозначениях получим:

G = kpiXi-i-k,j,X2~kocb pl = F{o).

1 Ki с.

Следовательно, в уравнениях (17.81) в данном случае имеем:

11= --у- 12-0>

й21=1,

С1 = А;рф,

22 = 0.

2 = кф,

6i= -

2 = 0, Г = кос-

Определитель (17.83) здесь будет

D{p) =

~р о

а корни его

;.1=-

;2=о.

Вычислив Nj (р) и N2 (р) согласно указанию к формуле (17.83), а также производную D {р) и коэффициенты р, Р2. h, h, по формулам (17.87) и (17.92), получим:

N,{p)==p, iv2(p)=4, D{p) = - + 2p, Pi = A;i(A:--) h=-kjci hi = ki, -kiTi.

В результате канонические уравнения (17.89) здесь будут

№ = /(а), (17.103)

po = ki /Сф--) Zi-kikz-1ocF (Р),

а выражения (17.91) для прежних переменных х, х, § через канонические % и Zg примут вид

xt = kiZi,~kiZs,

Х2 = -hTiZi + kiTiZz - kiy, ,

-kjey = kiTi(ki--) Zi + (kikpi-kiTik + кос) Zg-f ст.

Подставив Уа из последнего уравнения во второе и использовав (17.102),

получаем следуюшре выражения для исход- Еых переменных через канонические:

pikiizi - z), l = zz, Л

il==-[-pti,Zi+(A:iA:p-f A;oc)z2 + a]. j

(17.104)

Далее согласно (17.97) записываем уравнения для определения попупериода автоколебаний: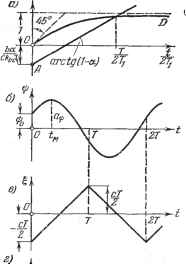

ii ckocTi где введено обозначение

(17.105)

(17.106)

Левая часть равенства (17.105) изображается прямой АВ (рис. 17.16, а), а правая Рис. 17.16. часть - кривой 0D. Точка пересечения их

является решением, уравнения (17.105). Из графика видно, что это уравнение имеет решение только при условии

~ оо < а < 1, (17.107)

причем

О < Г < оо.

При а > 1 прямая АВ не пересекается с кривой 0D, что означает отсутствие автоколебаний при этих значениях а.

Но кроме равенства (17.105) необходимо еш;е вьшолнение условия переключения (17.98), которое в данном случае будет

fcoc + №(fc. -)th<0.

a + th--а<0. (17.108)

Следовательно, если даже значение а лежит в интервале (17.107), но не выполняется условие (17.108), то автоколебаний в системе не будет.

Для исследования устойчивости автоколебаний запишем характеристическое уравнение (17.100). Оно получает здесь вид

Случай 1 Ч- р = О, когда знаменатель обрап;ается в нуль, нереален.

Поэтому, считая 1 -- р th ф О, приведем это уравнение к общему знаменателю, использовав обозначение (17.106), что дает

21 а * 27.

= 0.

Поскольку данное характеристическое уравнение имеет вторую степень, то для устойчивости исследуемых колебаний необходима и достаточна положительность его коэффициентов. Коэффициент при р положителен. Коэффициент при р согласно (17.107) тоже положителен. Поэтому условие устойчивости автоколебаний сводится к положительности свободного члена этого уравнения, т. е.

( + .)ctbi ±.bi,>0.

Отсюда с учетом (17.107) заключаем, что имеются две области устойчивых автоколебаний:

21 /

-оо<а<0 и , <а<1. (17.109)

Между ними лежит область неустойчивого периодического решения

Т \2

2ftoc

где при начальных условиях, приводящих к отклонениям, которые больше амплитуды этого периодического решения, в системе получаются расходящиеся, колебания.

Условие а < О, где всегда имеют место устойчивые автоколебания, согласно (17.106) означает

йрф > АЛф, (17.111)

т. е. неустойчивую систему (17.110) можно сделать устойчивой автоколебательной системой путем усиления интенсивности введения производной в закон регулирования согласно (17.111). При этом необходимо параметры системы подобрать так, чтобы добиться достаточно малого значения амплитуды автоколебаний и приемлемой (по техническим условиям) частоты их.