мы. Существуют, конечно, и такие функции V (ж, х, . . ., которые соответствуют всей области устойчивости.

2. К сформулированной выше теореме Ляпунова необходимо добавить, что понятие устойчивости по Ляпунову допускает, чтобы при знакоопределенной функции V производная от нее W была не обязательно знакоопределенной или знакопостоянной, а могла быть и тождественно равна нулю во всем рассматриваемом фазовом пространстве. В этом случае, проводя аналогичные, прежним рассуждения, легко убедиться, что изображающая точка М (рис. 17.10) будет оставаться все время на какой-нибудь одной из поверхностей V = const, куда ее забросили начальные условия. В результате система хотя и не будет асимптотически приближаться к установившемуся состоянию, но все же будет все время в достаточной близости от него.

Теорема Ляпунова о неустойчивости нелинейных систем. Поскольку предыдущая теорема Ляпунова дает, вообще говоря, только достаточные условия устойчивости и поскольку кроме области устойчивости нелинейная система может иметь целый ряд особых областей (см. § 16.1), то может возникнуть потребность в отдельном определении области неустойчивости путем использования нижеследующей теоремы Ляпунова, которая дает достаточные условия неустойчивости системы.

Теорема формулируется так: если при заданных в форме (17.46) уравнениях системы п-го порядка производная W (xi, х, . . ., Хп) от какой-нибудь функции Ляпунова V {х, х, . . ., ж ) окажется знакоопределенной, причем

сама функция V в какой-нибудь области, примыкающей к началу координат, будет иметь знак, одинаковый со знаком производной W, то данная система неустойчива.

Справедливость этой теоремы иллюстрируется геометрически следующим образом. Пусть для какой-нибудь заданной системы второго порядка (п = 2) найдена такая знакопеременная функция V (х, х), для которой производная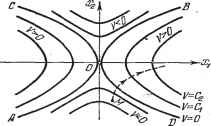

Рис, 17.11.

- Х,{х х,)-

Xs (a;i, жа) = W.{xi, x)

оказалась знакоопределенной положительной. Пусть при этом линии V {х, х на фазовой плоскости располагаются, как указано на рис. 17.11, где линии АВ и CD соответствуют значениям У = О и разделяют те области, внутри которых F > О и F < 0.

Возьмем изображающую точку М, как показано на рис. 17.11. Поскольку там F -< О и везде

=4>о.

то изображающая точка М с течением времени будет двигаться и пересекать линии F = С, переходя от меньших значений С к большим. Она может при этом лишь временно приблизиться к началу координат, но в конце концов будет неограниченно удаляться от начала координат. Это соответствует расходящемуся процессу, т. е. неустойчивости системы. Аналогично можно показать справедливость теоремы и для системы любого порядка п, проводя те же рассуждения для п-мерного фазового пространства.

Наиболее полно решение нелинейных задач теории регулирования с применением указанных теорем дано в известной книге А. И. Лурье [81],

Где предложено брать функцию Ляпунова в виде квадратичная форма плюс интеграл (см. также [98]).

Приведем два примера применения изложенных теорем Ляпунова к исследованию нелинейных систем автоматического регулирования.

Пример учета нелинейности привода регулирующего органа. Такой пример применительно к системе самолета с курсовым автопилотом (в упрощенном виде) был рассмотрен в работе А. И. Лурье и В. Н. Постникова. Схема данной системы автоматического регулирования представлена на рис. 17.12, а.

Регулируемый объект (самолет)

Свободный гироскоп

ЧЭ.П \у I

Скоростной И я

гироскоп

Регулирующий орган (руль)

глектро-деивашель

Жесткая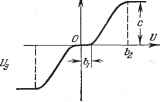

Рис. 17.12.

Пусть все звенья системы являются линейными, за исключением электродвигателя (с редуктором), для которого будем рассматривать его реальную характеристику (рис. 17.12, 6). Она может иметь произвольное криволинейное очертание с зоной застоя (при \ V \ <Ъ- и с зоной насыщения (при \и \ > Ь). Наклон характеристики и ее криволинейность могут быть любыми, лишь бы только соблюдались условия

dF dU

>0, F>0 при Z7>bi и F<0 при &i. (17.54)

Требуется найти условия устойчивости данной системы автоматического регулирования.

Уравнение самолета как регулируемого объекта в грубо упрощенном виде будет

{Тгр -М) РФ = -fci6, (17.55)

Где ф - отклонение курсового угла самолета, б - отклонение руля.

Уравнения чувствительных элементов (гироскопов с потенциометрами):

Уравнение обратной связи

Us = кЬ.

Уравнение усилителя

и = + keU - k-jUg. Уравнение электродвигателя с редуктром и рулем

pb = F{V),

где F {U) задается графиком рис. 17.12, б.

Уравнения (17.56), (17.57), и (17.58) можно свести к одному:

(17.56) (17.57) (17.58)

(17.59) (17.60)

кф - kjc, кр, - kgkg, кос - kjc-j. Для перехода к уравнениям вида (17.46) введем новые переменные:

3 Tifeifep т. безразмерное время

Tikikp

(47.61)

(17.62)

С введением этих переменных дифференциальные уравнения всей систет мы (17.55), (17.59), (17.60) преобразуются к виду (17.46), а именно:

-37-= -x + f{xs),

dx dxo

(17.63)

.з?де

fejfe

(17.64)

f{xs)=F{TihkpXs),

т. е. функция / (xg) имеет все те же свойства, что и заданная функция F {U) (рис. 17.12, б), и отличается лишь масштабом чертежа по оси абсцисс в связи с заменой переменной U на Xg согласно третьему из равенств (17.61).

Установившийся процесс полета при данной системе согласно (17.55), ;(17.59), (17.60) и графику рис. 17.12, б будет иметь место при

6=0, р=о, iK-,

(17.65)

т. е. наличие зоны застоя двигателя приводит к тому, что в установившемся процессе курсовой угол может принять любое постоянное значение в пределах (17.65).

В новых переменных (17.61) установившийся процесс полета определяется значениями:

xi = 0, Ж2 = О,

Tihkp

(17.66)

чему соответствует любая точка отрезка АВ в фазовом пространстве <рис. 17.13, а).

При отыскании условий устойчивости рассмотрим два случая: у > 1 и О < Y < 1. .

Случай у > i. Возьмем функцию Ляпунова в виде