dV dV dxi SV &2

dt dxi dt dt ~ dxn dt

TT dxi dXn

Подставив сюда значения -~-, . . ., из заданных уравнении системы-

регулирования в общем случае (17.46), получим производную от функции Ляпунова по времени в виде

-5Г=-й1+-&7+---+ (1>

где Xl, Zg, . . ., Хп - правые части уравнений (17.46) системы автоматического регулирования, представляющие собой заданные функции от отклонений Xl, 2, . . ., Хп-

Следовательно, производная от функции Ляпунова по времени, так же как и сама Y, является некоторой функцией отклонений, т. е.

=W{xuX2, Хп), (17.50)

причем согласно свойству (17.47) эта функция W, так же как и сама F,. тождественно обращается в нуль при == 2 = ... = ж = 0. Поэтому к ней в одинаковой степени можно применять все те же понятия знакоопределенности, знакопостоянства и знакопеременности в некоторой области вокруг начала координат, о которых говорилось выше по отношению к функции F.

Здесь шла речь только об уравнениях (нелинейных), в которые не входит в явном виде время t, так как только этот случай будет рассматриваться в дальнейшем. Вообще же метод Ляпунова может применяться и при наличии времени t в явном виде, в частности для уравнений с переменными коэффициентами (линейных и нелинейных).

Базируясь на этих предварительных сведениях, дадим общую формулировку теорем Ляпунова об устойчивости и неустойчивости нелинейных систем и покажем их справедливость. Теоремы эти годятся для исследования устойчивости систем регулирования не только при малых, но и при больших отклонениях, если для них справедливы исходные уравнения данной системы регулирования. Устойчивость системы при любых больших начальных отклонениях называется коротко устойчивостью в целом.

Теорема Ляпунова об устойчивости нелинейных систем. Теорема формулируется следующим образом: если при заданных в форме (17.46) уравнениях системы п-го порядка можно подобрать такую знакоопределенную функцию Ляпунова V {xi, 2, . . ., Хп), чтобы ее производная по времени W (ж, х, . . . . . ., ж ) тоже была знакоопределенной {или знакопостоянной), но имела знак, противоположный знаку V, то данная система устойчива. При знакоопределенной функции W будет иметь место асимптотическая устойчивость.

Проиллюстрируем справедливость этой теоремы на наглядных геометрических образах. Для простоты возьмем систему третьего порядка

взяты те отклонения переменных системы регулирования в переходном! процессе

Хг = Xl (t), х = х (t), . . ., Хп= Хп {t),

в которых, записываются уравнения (17.46) для этой системы. Производная от функции Ляпунова (17.48) по времени будет

(п = 3). Уравнения (17.46) для нее в общем виде будут

(17.51)

= Zi(xb Xz, Жз),

--г{х1, Xz, Жз),

= {1, Xz, Xg).

Возьмем знакоопределенную положительную функцию Ляпунова в виде

V = аж + feV, + cV (17.52)

где а, b, с - произвольно заданные вещественные числа. Будем придавать величине V возрастающие постоянные значения: F = О, С, Cz, Cg, . . ., что означает

axl + bxl + = О, gVj + b4 + cxl = Ci, axl + bxl -Ь-сж = Cz,

Первое из этих выражений соответствует одной точке ж = = = (началу координат фазового пространства), а остальные - поверхностям эллипсоидов в фазовом пространстве, причем каждый последующий эллипсоид содержит внутри себя целиком предыдущий (рис. 17.10).

Возьмем теперь производную от функции Ляпунова по времени. Согласно (17.49) и (17.52)

= 2aXiXi {xi, Xz, Жз) + 2bzXz {i, Xz, Жз) + 2cXsXs (xi, Xz, Xg) =

= W {xi, Xz, Жз),

где функции Xi, Xz, Xg берутся из заданных уравнений системы регулирования (17.51).

Если полученная таким путем функция W (ж, Xz, Жд) окажется знакоопределенной отрицательной, т. е. если

4<0 (17.53)

во всех точках исследуемого фазового пространства, кроме одного только начала координат, где

= 0 (при Ж1 = Ж2 = Жз=0),

то при любых начальных условиях изображающая точка М (рис. 17.10) вследствие (17.53) будет двигаться в сторону уменьшения значения V, т. е. будет пересекать эллипсоиды, изображенные на рис. 17.10, извне внутрь. В результате с течением времени изображающая точка М будет стремиться к началу координат О фазового пространства и уже никак не сможет выйти за пределы тех эллипсоидов, в которые она проникла.

Это и означает затухание всех отклонений ж, Xz, х в переходном процессе с течением времени. Таким образом, установлена устойчивость данной системы регулирования, что иллюстрирует справедливость теоремы для системы третьего порядка (в случае знакоопределенной функции W).

Отсюда вытекает справедливость теоремы и в общем случае. Рассуждения остаются аналогичными, только вместо трех уравнений (17.51) будет п уравнений (17.46). Как и раньше, для любой знакоопределенной положи-

Mq точные методы исследования устойчивости и автоколебаний гл. 17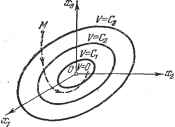

тельной функции Ляпунова F (ж, Xg, . . ., ж ) = С получим некоторые замкнутые поверхности, окружающие начало координат (рис. 17.10), но уже не в обычном трехмерном, а в п-мерном фазовом пространстве (их иногда

называют гиперповерхностями). Поэтому, если производная =

= W {х, х, . . ., Жп) окажется знакоопределенной отрицательной, то траектория изображающей точки М в п-мерном пространстве при любых начальных условиях с течением времени будет пересекать указанные поверхности только извне внутрь, что и свидетельствует об устойчивости данной системы.

Если же функция W будет не знакоопределенной, а знакопостоянной, то очевидно, что траектория изображающей точки М не везде будет пересекать поверхности V = С, а может их касаться в тех точках, где W обращается в нуль (помимо начала координат). Но так как Рис. 17.10. во всех других местах фазового пространства

функция Поимеет один и тот же знак, вследствие чего изображающая точка может идти только извне внутрь поверхности F = С, то при решении задачи остается только проверить, не застрянет ли изображающая точка там, где = О (см. пример ниже).

Замечания к теореме Ля&унова об устойчивости. По поводу сформулированной теоремы Ляпунова об устойчивости системы необходимо сделать следующие два важных замечания.

1. В теореме речь идет о подборе функции Ляпунова F (ж, х, . ., ж ). Вообще говоря, при заданных в форме (17.46) уравнениях системы регулирования можно подобрать несколько различных вариантов функции F, поскольку требуется только знакоопределенность ее и ее производной. Различные варианты функции F, удовлетворяющие теореме, могут дать соответственно различные варианты условий устойчивости для одной и той же системы регулирования. При этом одни из них будут шире, другие уже, последние могут входить в первые как частный случай и т. д.

Поэтому, вообще говоря, данная теорема Ляпунова обеспечивает получение достаточных условий устойчивости, которые не всегда будут и необходимыми, т. е. при выполнении условий теоремы система наверняка будет устойчивой, но эти условия могут не охватывать всей области устойчивости системы по параметрам. В самом деле, если выбрана функция U, удовлетворяющая теореме, нет уверенности в том, что нельзя подобрать другой вариант функции F, который бы еще более полно охватывал область устойчивости данной системы.

Геометрически это значит, что, получив определенное семейство поверх-костей V = С (рис. 17.10) и убедившись, что траектории изображающей точки М приближаются к началу координат, пересекая эти поверхности извне внутрь, нельзя быть уверенным в том, что не существует еще других вариантов траекторий изображающей точки М, которые в отдельных местах могут пересекать данные поверхности изнутри вовне, но все же с течением времени в конце конйов неограниченно приближаться к началу координат. Такие траектории будут соответствовать другому семейству поверхностей F = С, т. е. другому варианту выбора функции Ляпунова.

В ряде технических задач можно вполне удовлетвориться этими достаточными условиями устойчивости. От более или менее удачного подбора функции Ляпунова F будет зависеть большая или меньшая близость полученных достаточных условий устойчивости к необходимым и достаточным, 5г. е. более или менее полный охват всей области устойчивости данной систе-