Наконец, на рис. 17.7, гид изображены случаи, когда на диаграмме точечного преобразования кривая \ \ = f {xq) не пересекается с прямой, проведенной под углом 45° к осям. Это означает соответственно устойчивость (г) и неустойчивость {д) системы при любых начальных условиях (до которых справедливы исследуемые уравнения системы).

Заметим, что изложенное выше является лишь качественным рассмотрением, так как в нем отсутствует время t. Остается неизвестным течение процессов во времени, период (частота) автоколебаний. Чтобы получить

npeuiiiuaii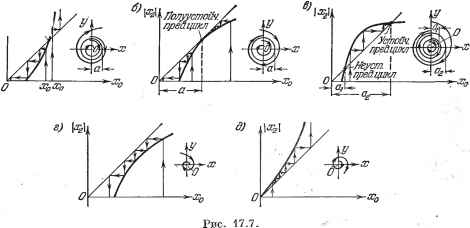

полное решение задачи, нужно к данному рассмотрению добавить епе решение дифференциальных уравнений на отдельных участках во времени (как Б методе припасовывания, см. § 16.1). Поэтому в методе точечного преобразования вводится соответствуюп];ИЙ временной параметр (здесь это не рассматривается).

Для систем выше второго порядка вместо фазовой плоскости придется иметь дело с фазовым пространством и с точечным преобразованием не линий, а поверхностей. Там появляются новые особенности процессов. Однако ввиду чрезвьшайной сложности таких построений рассматривать их не будем.

Метод изоклин. Выше были рассмотрены такие примеры нелинешых систем второго порядка, для которых фазовые траекторий легко находятся интегрированием уравнений по участкам. В тех случаях, когда внтегрирова-ние затруднено, ход фазовых траекторий, хотя бы качественно, можно проследить с помощью так называемого метода изоклин (без интегрирования уравнений). Количественно этот способ имеет меньшую точность. Применение его тоже ограничено системами второго порядка.

Изоклиной называется такая линия, во всех точках пересечения которой с фазовыми траекториями последние наклонены под одним и тем н е определенным углом к оси абсцисс х. Так, если известно дифференциальное уравнение фазовых траекторий

то для получения изоклины нужно положить

(17.44)

- с.

Уравнение изоклины, следовательно, будет

f{x,y) = c,

где с обозначает определенный тангенс угла наклона фазовых траекторий. Каждому заданному значению с соответствует своя изоклина. . Например, часто встречается нелинейное уравнение

которое можно записать в виде

dy dt

тогда дифференциальное уравнение фазовых траекторий будет выглядеть так: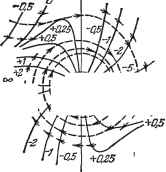

dy dx

= k{l-x)-f.

а уравнение изоклин

к{1~х)~~=с.

jHR * Задавая различные значения с (при

Jy(/\\x£l/ заданном к), для каждого из них строим

по этому уравнению кривую на фазовой плоскости - изоклину (сплошные кривые на рис. 17.8). Затем на каждой кривой наносим стрелочки под углами а = arctg с к оси абсцисс (на рис. 17.8 указаны зна-Рис. 17.8. чения с для каждой кривой). Из этих стре-

лочек и составляются искомые фазовые траектории; некоторые из них изображены на рис. 17.8 пунктиром. В данном случае получается устойчивый предельный цикл, что соответствует автоколебаниям в системе.

§ 17.2. Теоремы прямого метода Ляпунова и их применение

Предварительно заметим, что при изложении прямого метода Ляпунова, именуемого также второй методой Ляпунова, будем пользоваться дифференциальными уравнениями автоматической системы в форме уравнений первого порядка, полагая, что они записаны для переходного процесса в отклонениях всех переменных от их значений в установившемся процессе при новых постоянных значениях возмущающего / = / и задающего g ~ воздействий. Следовательно, эти уравнения для нелинейной системы п-го порядка будут:

r = Xi{xi, х, .... Хп),

dx dt

= Ха(i, 2, Хп),

~- - Хп {Xi, Х2, . . ., Хп),

(17.46)

где функции Xl, Х, . . ., Z произвольны и содержат любого вида нелинейности, но всегда удовлетворяют условию

так как в установившемся состоянии все отклонения переменных и их производные равны, очевидно, нулю по самому определению понятия этих отклонений.

Нам понадобятся в дальнейшем eni;e следуюпие сведения. Понятие о знакоопределенных, знакопостоянных и знакопеременных функциях. Пусть имеется функция нескольких переменных

V = V{xi, Xz, . . ., Хп).

Представим себе п-мерное фазовое пространство (см. § 16.1), в котором х, Xz, . . ж являются прямоугольными координатами (это будут, в частности, фазовая плоскость при п = 2 и обьшное трехмерное пространство при и = 3). Тогда в каждой точке указанного пространства функция V будет иметь некоторое определенное значение. Нам понадобятся в дальнейшем функции V (xi, Xz, . . Жп), которые обраш;аются в нуль в начале координат (т. е. при Xi = Xz - . . . = = 0) и непрерывны в некоторой области вокруг него.

Функция V называется знакоопределенной в некоторой области, если она во всех точках этой области вокруг начала координат сохраняет один и тот же знак и нигде не обра-

Рис. 17.9.

щается в нуль, кроме только самого начала координат.

Функция V называется знакопостоянной, если она сохраняет один и тот же знак, но может обрап];аться в нуль не только в начале координат, но и в других точках данной области.

Функция V называется знакопеременной, если она в данной области вокруг начала координат может иметь разные знаки.

Приведем примеры всех трех типов функций . V. Пусть и = 2 и

V = х1 -{- х1. Это будет знакоопределенная (положительная) функция, так как F = О только тогда, когда одновременно ж = О и Xg = О, и F > О при всех веш;ественных значениях х и Xz- Аналогично при любом п функция

V = х1 1 -\- ... -f ж . будет знакоопределенной положительной, а V = - {х -{- х1 -{-... -\- Хп) - знакоопределенной отрицательной.

Если взять функцию V = 3 -{- х1 при п = 3, то она уже не будет знакоопределенной, так как, оставаясь положительной при любых х, Xz и Xg, она может обрап1;аться в нуль не только при х = Xz = х = О, но также и при любом значении х, если х = Xz = О (т. е. на всей оси Хд, рис. 17.9, а). Следовательно, это будет знакопостоянная (положительная) функция.

Наконец, функция V = х Xz будет знакопеременной, так как она положительна для всех точек плоскости справа от прямой х = -Xz (рис. 17.9, б) и отрицательна слева от этой прямой.

Заметим, что в некоторых частных задачах нам понадобится также функция V, которая обраш;ается в нуль не в начале координат, а на заданном конечном отрезке АВ (рис. 17.9, в). Тогда знакоопределенность функции V будет обозначать ее неизменный знак и необрап1;ение в нуль в некоторой области вокруг этого отрезка.

Функция Ляпунова и ее производная по времени. Любую функцию

V V {х, Xz, . . ., Xji),

(17.48)

тождественно обрап1;аюп1;уюся в нуль при х- = Xz = ... = а; = О, будем называть функцией Ляпунова, если в ней в качестве величин ж, Xz, . . ., ж