ПЛОСКОСТИ (рис. 17.3, б). Аналогичная полоса HGGH будет и в нижней части плоскости. Все остальное заполняется такими же кривыми, как на рис. 17.3, а. Б результате с увеличением зоны нечувствительности размеры предельного цикла, а значит, и амплитуда автоколебаний уменьшаются. При = О предельный цикл вырождается в точку О.

При дальнейшем увеличении зоны нечувствительности характеристика нелинейного звена и картина фазовых траекторий принимают вид, показанный на рис. 17.3, е. Здесь автоколебания отсутствуют и становится устойчивым установившийся процесс с постоянным значением iJ). Ранее неустойчивый

особый отрезок FG теперь стал устойчивым. Дальнейшее увеличение зоны нечувствительности приводит к расширению отрезка FG, т. е. к увеличеншо установившейся ошибки системы из-за слишком широкого участка равновесия.

Пример 4. Рассмотрим вибрационный регулятор напряжения уравнения которого были составлены в § 16.2, а именно:

(Г1Р + 1)АС/= ~hAr,

причем уравнение нелинейного звена (регулирующего органа)

Аг, 1

(17.24)

Аг = г± sign (А/2 - н) при Дг = п sign (Д/2 -Ь ia) при

dt dt

>о

<0.

(17.25)

В качестве ординаты фазовой плоскости здесь удобнее взять не скорость

отклонения регулируемой величины , как делалось раньше, а вторую переменную A/j. Итак, примем для этой задачи

X = AU, у = A/g. Тогда уравнения (17.24) преобразуются к виду

--=-(j/-M,

где согласно (17.25), (17.26) и (17.28) имеем

Ar = risign(y -ii) при у<:кх, Ar = risign(y-f й) при y>kzx

(17.26)

(17.27) (17.28)

следовательно, первое из этих условий имеет место ниже прямой ВБ (рис. 17,4), а второе - выше нее. В первом случае переключение реле происходит при у = - ij, т. е. на прямой CD (рис. 17.4), а во втором случае - при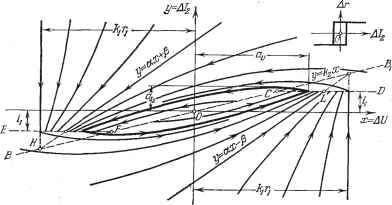

Рис. 17.4.

у = -ц, т. е. на прямой EF. Чертеж сделан в предположении, что kikr > i. В результате получаем, что выше линии EFCD будет

Дг = Г1, (17.30)

а ниже линии EFCD

Дг = -Г1. (17.31)

Рассмотрим сначала верхнюю область. Для нее, деля (17.28) на (17.27), с учетом (17.30) получим уравнение фазовых траекторий

dy Ti y-hx

(17.32)

Га x+hiri которое можно представить в виде

dy Tj y + kjkin - kzjx-j-lciri) dx T2 x-{-kiri

и проинтегрировать, применив вспомогательную подстановку

у + kjir =z(x + kj-j),

где z - новая переменная вместо у. В результате найдем следуюп;ее уравнение фазовых траекторий (при Ti > Т)-

у = ax + P + Ci{x + Vi) (Т > 1), (17.33)

где Ci - произвольная постоянная.

kikrj

Ti - T2 Ti~T2 Т2

(17.34)

(при 7 = 1 решение будет иметь другой вид, а при у <Z i будет а <; О и р < 0; эти решения не будут исследоваться).

Чтобы представить себе всю совокупность фазовых траекторий, можно провести на фазовой плоскости прямую

У1 = ах + (17.35)

и ко всем ординатам этой прямой добавлять

где а и Р определяются формулами (17.34). Амплитуда же будет немного больше ij.

Пример 5. Рассмотрим следящую систему с сухим трением в управляемом объекте, для которой уравнения были написаны в § 16.3. Уравнение регулируемого объекта (16.52) как нелинейного звена при отсутствии линейного трения (cj = 0) имеет вид

Jp-csigap = Ciin при рфО или рР = 0 и я>-,

Р = const при рР = о и 1 Jfl 1 <

придавая Cj произвольные значения (каждому значению будет соответствовать определенная фазовая траектория). Это будут параболы степени у с осью

X = -кг (17.37)

и с единым началом в точке Н (рис. 17.4), имеющей координаты

X = -к--1, у = -k-jkr-j.

На рис. 17.4 показаны все ветви этих парабол, лежащие выше линии EFCD (так как только там справедливы данные выкладки). Направления стрелок на полученных фазовых траекториях определяются тем, что проекция ско-

рости изображающей точки = справа от прямой (17.37) согласно (17.27)

будет отрицательна, а слева - положительна; проекция же Vy = согласно (17.28) выше прямой у = к будет отрицательна, а ниже - положительна (во всех точках прямой у = к касательные к фазовым траекториям горизонтальны).

Аналогично строятся и все фазовые траектории ниже линии EFCD, так как их дифференциальное уравнение отличается от (17.32) только заменой -\-г на -согласно (17.31).

В результате на рис. 17.4 видим, что все фазовые траектории, исходящие из особого отрезка FOC, расходятся, а все траектории, идущие от краев чертежа, сходятся. Как те, так и другие асимптотически приближаются к установившемуся предельному циклу, обозначенному на чертеже жирной замкнутой кривой (чичевицеобразной). Это соответствует тому, что установившийся процесс в системе является автоколебательным, причем размеры предельного цикла и aj представляют собой амплитуды автоколебаний соответственно регулируемого напряжения АС/ и тока в обмотке электромагнита реле A/g.

Определить фазовую траекторию, образующую этот предельный цикл, можно как такую кривую (17.33), у которой

{x)y=ii = - (a;)y= ij, (17.38)

чем определяется значение произвольной постоянной С. Значение х (17.38) для этой кривой и дает искомую амплитуду а- Амплитуда же ai определяется как ордината пересечения кривой предельного цикла с прямой у = к (ибо, как было показано ранее, в точках этой прямой касательные к фазовым траекториям горизонтальны).

Из чертежа (рис. 17.4) видно, что предельный цикл лежит левее точки L и охватывает точку С. Поэтому xq <С Ujj <i xj т. е. амплитуда автоколебаний регулируемого напряжения заключена в интервале