Уравнение регулятора (системы стабилизации) запишем в виде

М = МФ (ф, (О), (17.12)

где М-г - постоянная положительная величина, Ф (ф, о) - нелинейный закон регулирования, осуп;ествляемый при помощи логического устройства

по тому же простейшему принципу, что и на рис. 16.26, с той лишь разницей, что по углу ф фазовая плоскость ограничена значениями +я и -я, так как это составляет один полный оборот тела (рис. 17.2).

Изобразим процесс регулирования на фазовой плоскости. Уравнение всей системы согласно У (17.11) и (17.12) будет

= сФ(ф,о)), (17.13)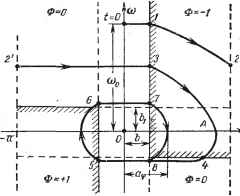

где обозначено

Рис. 17.2.

причем с имеет физический смысл величины углового ускорения, сообщаемого данному телу постоянным моментом Mj.

Умножив почленно уравнение (17.13) на выражение

получим дифференциальное уравнение фазовой траектории

(odco = сФ (ф, О)) йф.

(17.14)

Это уравнение легко интегрируется внутри участков, на которых Ф = const. В результате для кансдого отдельно взятого участка уравнение фазовой траектории будет

-=сФ(ф-фн), (17.15)

где фн и (Од - значения ф и о) в начальной точке данного участка. Зададим начальные условия процесса:

Ф = О, со = о при f = 0.

Для данной начальной точки процесса (см. рис. 17.2) имеем Ф = 0. Поэтому на первом участке процесса согласно (17.15) уравнение фазовой траектория будет

О) = const = о-

Этот участок движения с постоянной скоростью заканчивается в точке 1 (рис. 17.2), где происходит включение исполнительного органа (Ф = -1). Следовательно, для второго участка процесса (после точки 1) из (17.15) получим уравнение фазовой траектории

0)2 = со2 2с (ф - Ъ), (17.16)

так как в начальной точке 1 этого участка фн = fe, н = <о- Фазовая траектория (17.16) - парабола, ось которой совпадает с координатной осью ф.

2 = 1 о-2с(я-Ь). (17.17)

Это значение переносим в точку 2 (для вращающегося тела ф = ± - это одна и та же точка). Здесь происходит выключение исполнительного органа (Ф = 0). Поэтому дальнейшее движение согласно (17.15) пойдет с постоянной скоростью

О) = const = СОо

до точки 3 (рис. 17.2). Таким образом, в рассмотренной начальной части процесса регулирования тело совершило один полный оборот, но в конце этого оборота скорость вращения его стала меньше начальной.

В точке 3 снова включается исполнительный орган (Ф = -1), в результате чего фазовая траектория будет

0)2 = о) - 2с (ф - Ъ), , (17.18)

так как в точке 3 фц = Ъ, ц = < 2- Допустим, что соответствующая уравнению (17.18) парабола 3-4 не доходит до границы ф = я. Это означает, что тело больше не совершит полного оборота, а начнет (с точки А) возвращаться в сторону нулевого положения.

В точке 4 (рис. 17.2) имеем скорость 4 = -Ъ-. Следовательно, из (17.18) угловая координата ее будет

Ф4 = Ь +

где 2 определяется по формуле (17.17). Дальше {4-5) процесс пойдет с постоянной скоростью (так как Ф = 0), после чего тело войдет в установившийся автоколебательный режим, определяемый предельным циклом {5-6-7-8). Уравнение параболы 7-8 согласно (17.15) будет

-2-=-с(ф-Ь).

Отсюда амплитуда угловых автоколебаний Яф, как значение ф при о = О, будет

= & + . (17.19)

а амплитуда колебаний скорости

Сщ = fej.

Она равна зоне нечувствительности измерителя угловой скорости fe, в то время как амплитуда угловых колебаний (17.19) несколько больше зоны нечувствительности измерителя угла Ъ.

Период автоколебаний 4 можно вьпшслить как сумму времен:

~ хол ~Ь pa6i

где хол И fpa6 - времена участков (б-7) -- (8-5) и (5-6) -\- (7-8) соответственно. По законам равномерного и равнозамедленного движений соответственно получаем

Это соответствует равнозамедленному движению = -с) Изображая

параболу графически, доводим ее до границы ф = я (участок 1-2 на рис. 17.2), причем в точке 2 согласно (17.16)

(17.22)

Итак, установившийся режим стабилизации в данной системе является автоколебательным. Однако уравнение системы (17.13) справедливо только для идеальной системы стабилизации. Всякое реально имеюп;ееся запаздывание в работе усилительно-преобразовательного и исполнительного устройств приведет к увеличению амплитуд автоколебаний по сравнению С полученными здесь значершями. Решение задачи с учетом постоянных времени системы управления будет дано в следуюп;ей главе.

Пример 3. Уравнения системы автоматического регулирования курса водяной торпеды в упроп;енном варианте имеют вид: линейная часть (16.40) и (16.41), т. е.

Tjjphp +pip = -Лб, S = Лгф, (17.20)

и нелинейное звено (возьмем сначала один случай - рис. 16.18, е)

6=csign(s -Ь) при ps>0, I

6 = csign(s-f fe) при ps<0. J К >

Покажем, что здесь равновесное установившееся состояние системы с постоянным значением ф = О неустойчиво, но будет иметь место устойчивый автоколебательный процесс.

Возьмем фазовую плоскость (х, у) с координатами а; = ф, у = /гф (угол отклонения и угловая скорость отклонения оси торпеды от заданного курса). Уравнения (17.20) и (17.21) перепишутся в виде

dy у kj

dt ~-У dt 2-1 Ti

6 = csign (ж-при y>0,

6 = csign (ж-Ь-) при y<0.

Из сравнения этих уравнений с упрощенными уравнениями системы регулирования температуры в конце § 16.1 видна их полная аналогия. Поэтому здесь, так же как и в случае рис. 16.15, установившийся процесс движения торпеды будет автоколебательным, причем картина фазовых траекторий будет иметь вид, показанный на рис. 17.3, а.

При этом кривая АВ предельного цикла, соответствующая автоколебательному процессу, определяется из уравнения (16.31) с таким значением произвольной постоянной С, чтобы выполнялось условие

Уа~Ув, т.е. {у) ь=-(у) ь, (17.23)

X- X--~т-

так как только в этом случае и получится замкнутая кривая предельного цикла ABD (рис. 17.3, а). Определив таким образом С, найдем амплитуду автоколебаний а как значение х при у = О, т. е. согласно (16.31)

а = kcTi In кс -Ь С.

Значения же (17.23) дают амплитуду q колебаний скорости у. Можно все это определять и графически прямо по чертежу (рис. 17.3, а). Период автоколебаний остается неизвестным.

Введем теперь в характеристику нелинейного звена (рулевой машинки) зону нечувствительности, как показано на рис. 17.3, б, е. Так, на том участке характеристики б = / (s) (рис. 17.3, б), где 6 = 0, из (17.22) следует, что

у=-- + С2,

что соответствует наклонным прямым внутри полосы EFFE на фазовой