ГЛАВА 17

ТОЧНЫЕ МЕТОДЫ ИССЛЕДОВАНИЯ УСТОЙЧИВОСТИ И АВТОКОЛЕБАНИЙ

§ 17.1. Фазовые траектории и метод точечных преобразований

Понятие о фазовом пространстве, о фазовых траекториях и их типах было уже дано выше. В данном параграфе на примерах построения фазовьпс траекторий для простейших систем второго порядка будут проиллюстрированы некоторые важные особенности процессов в нелинейных системах автоматического регулирования.

Пример 1. Возьмем систему автоматического регулирования с объектом без самовыравнивания и с приводом регулируюпцего органа, имеюпщм постоянную скорость. Уравнение регулируемого объекта без самовыравнивания будет

TaPf = I. . (17.1)

Для регулятора без массы и демпфера с жесткой обратной связью, т. е. при бг] = -ф, о = т] - , 1=1, получим

ст=-ф-1, (17.2)

где ф. г], I, и о - относительные изменения регулируемой величины, смещений чувствительного элемента, регулирующего органа, элемента обратной связи и управляющего золотника (рис. 10.11, а), б - коэффициент. Привод регулирующего органа пусть имеет постоянную скорость в двух вариантах: 1) с мгновенным переключением (рис. 16.22, ж) при переходе управляющего элемента (золотника струйной трубки) через нейтральное положение (о = 0); 2) с зоной нечувствительности (рис. 16.22, з) вследствие наличия перекрытия золотника или струйной трубки. В первом случае уравнение привода регулирующего органа будет

р1 = с sign о, (17.3)

а во втором

р1 = 0 при с<Ь,

р1 = с sign а при I о I > Ь.

(17.4)

Возьмем фазовую плоскость (х, у), приняв

а; = Ф, I/ = рф. - (17.5)

Из уравнений (17.1), (17.2) и (17.5) имеем

1 = ТаУ, 0=-Х~ТаУ. (17.6)

Следовательно, переключения привода в первом варианте (о = 0) будут

иметь место при

а: = -8ТаУ,

(17.7)

что соответствует прямой АВ (рис. 17.1, а) на фазовой плоскости, причем согласно (17.16) значениям о > О соответствует часть плоскости слева от прямой АВ, а о < О - справа.

На основании первого из соотношений (17.6) с учетом (17.3) при о < О получаем

dy с

а из (17.5)

откуда находим уравнения фазовых траекторий

dy с

(17.8)

(17.9)

(17.10)

или, после интегрирования.

Это~есть семейство парабол, показанное на рис. 17.1, а справа от линии АВ (они симметричны относительно оси х). Так как (17.8) и (17.9) являются лроекциями скорости v изображаюш;ей точки М на оси хжу,10 имеем Vy < G,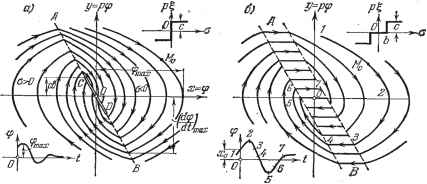

Рис. 17.1.

а знак 17совпадает со знаком у.Ъ соответствии с этим на рис. 17.1, а укажем стрелочками направление движения изображающей точки М по фазовым траекториям. Аналогичным путем легко строятся параболы слева от прямой АВ.

В результате, как видно из общего расположения фазовых траекторий (рис. 17.1, а), получается устойчивая система с затухающим колебательным переходным процессом. Но число колебаний будет конечным. В самом деле, здесь имеется особый отрезок CD, в который вливаются все фазовые траектории. Чтобы выявить поведение системы на этом отрезке, вспомним, что для него согласно (17.7) и (17.5)

баФ + Ф = 0, . или =,С.2,е

Следовательно, попав на отрезок CD, изображающая точка не может с него уйти, и система будет апериодически приближаться к установивше-

муся состоянию, т. е. изображающая точка будет сползать по отрезку CD к началу координат О. Таким образом, имевший место вначале колебательный переходный процесс после конечного числа колебаний вырождается в этот так называемый скользящий процесс.

Крайние точки особого отрезка CD определяются, очевидно, как точки, в которых прямая АВ касается одной из парабол соответственно правого

и левого семейств. Поэтому, подставив значения из (17.7) в выражение

(17.10), найдем точку С:

Ус = сЬ.

По найденной картине расположения фазовых траекторий можно качественно представить себе кривую переходного процесса ф (f) при любых начальных условиях. Начальными условиями определяется начальное положение изображающей точки М и тем самым - определенная фазовая траектория, иллюстрирующая протекание процесса. Она показывает (рис. 17.1, а) максимальное отклонение регулируемой величины фшах максимальную скорость (рф)п1ах такжо все последующие отклонения, число колебаний и т. п.

Рассмотрим теперь ту же систему, но с учетом зоны нечувствительности. В этом случае переключениям привода (при а = -Ъ и о = -\-Ъ) на фазовой плоскости соответствуют согласно (17.6) две наклонные прямые (рис. 17.1, б):

X = -ЬТаУ + ЬЬ ж х = -ЬТаУ - ЪЬ.

Между этими прямыми о < fc, правее их о < -Ъ, левее их о > fc (причем Ъ > 0).

При I о I < fc из (17.4), (17.6) и (17.5) получаем

dy г. dx

откуда (при уфО) .

-=0, или ,у = Сз

(прямые, параллельные оси х в полосе АВ на рис. 17.1, б).

При I о I > fc получим прежние параболы. В результате снова система оказывается устойчивой и имеет колебательный переходный процесс,но вместо особой точки О получаем особый отрезок {у = О, -ЬЬ < а; < 66), т. е. установившееся состояние определяется неоднозначно. Это соответствует тому, что регулятор может находиться в равновесии в любом месте внутри зоны нечувствительности. Здесь точно так же возможен скользящий процесс, как и в случае рис. 17.1, а.

В данном примере система оказывается устойчивой при любых значениях параметров и при любых начальных условиях. Однако здесь для получения системы второго порядка была проведена грубая идеализация уравнений регулятора (пренебрежение массой и демпфированием).

Пример 2. Допустим, что требуется стабилизировать угловое положение некоторого тела, когда сопротивлением среды его вращению можно пренебречь. Уравнение объекта будет

(17.11)

где / - момент инерции тела, ф - угол поворота тела, о - его угловая скорость, М - управляющий момент со стороны исполнительного органа системы стабилизации.