(16.62)

Уравнение привода регулирующего органа с учетом указанных обстоятельств вместо прежнего линейного будет иметь нелинейный вид:

. pl = F{s), . (16.60)

где F (s) есть нелинейная функция задаваемая графиком (рис. 16.22, а или г). Для электрических приводов можно записать

р1 = F (i). (16.61)

В приближенном кусочно-линейном виде (рис. 16.22, б) уравнение (16.60) записывается следующим образом:

р1 = 0 при -bis+bi,

pl = h{s~bi) при +fci<s<-l-b2, pl = kc{s + bi) при -bi>s> -Ьа. pl = csigns при )sl>b2-В случае наличия гистерезиса (рис. 16.22, д) придется написать два ряда таких же выражений с разными значениями Ь ш Ь - один для движения вправо (ps > 0) и другой для движения влево (ps << 0). Этим определяется уравнение привода регулирующего органа как нелинейного звена. Уравнение линейной части составляется обычным способом в зависимости от того, в какой конкретно автоматической системе этот привод применен.

Следящая система с линейным и квадратичным трением. В § 16.3 была рассмотрена следящая система с линейным и сухим трением. Пусть теперь управляемый объект в той же следящей системе обладает кроме линейного

еще квадратичным трением, т. е. уравнение объекта имеет вид

-Лвр = CiH, Мч = Сгрр + Cs (рр) sign р

(рис. 16.23). Тогда уравнение управляемого объекта как нелинейного звена будет

{Jp + с) рр + сз (рР)2 sign рр = cii . (16.63)

Уравнение линейной части системы в полном виде по-прежнему будет (16.53).

Система автоматического регулирования с переменным коэффициентом усиления. В ряде случаев для повышения качества процесса регулирования бывает желательно, чтобы воздей-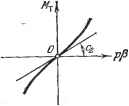

Рис. 16.23.

ствие на регулируемый орган было не пропорциональным отклонению регулируемой величины, а усиливалось или ослаблялось при увеличении этого отклонения (нелинейный закон регулирования). Примерами такого воздействия с переменным коэффициентом усиления могут служить характеристики с ограниченной линейностью или с насыщением (рис. 16.22, а). Однако они дают уменьшение коэффициента отклонения. Рассмотрим теперь два примера ньш коэффициентом усиления, который отклонения.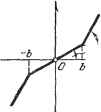

arctgk

arctgh

Рис. 16.24.

усиления при увеличении характеристик с перемен-увеличивается при увеличении

Уравнение нелинейной части привода регулирующего органа будет в случае характеристики рис. 16.24, а

pl==hs при s<fc, р=кф + к1{8-Ъ) при s>b,

~кф-\-к1{8-\-Ъ) при s< -fc.

(16.64)

(16.65)

объект

измерители

Логичеокое устройстбо

Усипитепь-

UcnojiHumemoe устройстбо

Рис. 16.25.

а в случае характеристики рис. 16.24, 6

Pl-F (s).

Все рассмотренные примеры иллюстрируют случай, когда общая схема системы имеет вид рис. 16.1, т. е. случай нелинейной системы первого класса (кроме случая сухого трения в следящей системе при наличии остановок). Комбинации нелинейностей приводят к нелинейным системам второго и третьего классов (см. главу 18).

Система автоматического регулирования с логическим устройством. Пусть динамика регулируемого объекта (рис. 16.25) описывается уравнением

{ТоР + 1)Р = к. (16.66)

Уравнения измерителей

{Тр + 1) и = Кх, (TzP + i)v = kzpx. (16.67)

Уравнение усилителя-преобразователя с логическим устройством 2,

{TsP + 1) I/ = йз Ф (и, V). (16.68)

Уравнение исполнительного устройства

{Т + i)z = -ку. (16.69)

Кроме того, должна быть задана логика формирования нелинейного закона регулирования Ф {и, v), которая может быть назначена или синтезирована в очень разнообразных формах для обеспечения простоты и наденности аппаратуры, наибольшего быстродействия, наименьшей затраты энергии на управление, учета ограничения мощности] источника энергии и специфики желательных режимов его работы и т. п.

Выбранную тем или иным образом логику формирования нелинейного закона управления можно записывать в аналитической форме. Однако во многих случаях удобнее изображать ее графически на плоскости входных величин логического устройства {и, V).

Для примера рассмотрим простейшую логику (рис. 16.26): Смысл ее заключается в следующем. Величины и и v, согласно уравнениям (16.67), отечностью до постоянных времени соответствуют отклонению регулируемой величины X я ее первой производной по времени рх. Поэтому наличие порогового значения щ соответствует тому, что при малых х исполнительное Згстройство не работает (ф = 0). Не работает оно также и при больших отклонениях х, но только тогда, когда шнеется достаточная по величине скорость рх (соответствующая превышению порога ± 1;) со знаком, противо-

Ф=-1

Рис. 16.26.

Бис ~1Г

i

положным знаку х, ибо в этом случае отклонение х уменьшается по величине само собой даже при неработающем исполнительном устройстве системы управления. Исполнительное устройство включается (Ф = или Ф = -1,

рис. 16.26) только тогда, ког-КЭ \ да при достаточно больших

отклонениях х {\и \ >и скорость рх имеет тот же знак (т. е. отклонение возрастает по величине) либо когда скорость рх имеет противоположный знак, но мала { < v.

Система с переменной структурой. Как уже указывалось в начале книги (§ 2.3), системы с переменной структурой содержат в себе специальное переключающее устройство для изменения структуры регулятора, которое срабатывает в зависимости от размеров и знаков входных величин.

Примеры переключающих устройств приведены схематически на рис. 16.27, где КЭ - ключевой элемент, БИС - блок изменения структуры. Уравнение принято [42] записывать в виде.

и = (16.70)

Функция Ч* может строиться по-разному. Например (рис. 16.27, а),

=1: (16.71)

I Р при xix<:0.

Для случая, указанного на рис. 2.9 и 2.10, будем иметь (рис. 16.27, б)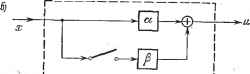

Рис. 16.27.

(16.72)

при X<iXj, при X > Xj.

Под символами сх и р могут также иметься в виду различные выражения:

в простейшем случае постоянные

а = ki, р = /сг,

в другом случае

а = /с р = кр.

(16.73) (16.74)

и любые другие; в том числе и нелинейные.

Основная же характерная нелинейность здесь состоит в самом факте автоматического переключения в зависимости от состояния входных величин.