Регулирующий орган (контакты К, скачком включающие и выключающие сопротивление 2г является нелинейным звеном релейного типа. Выходная величина его - сопротивление г цепи возбуждения - меняется скачкообразно при срабатывании

Е F

6J л

! I

Рис. 16.17.

и отпускании реле, т. е. в зависимости от величины тока /а в цепи катушки 2 электромагнитного реле. Это изображено на рис. 16.17, а, где /ср и /отп - токи полного сра-батывания и отпускания реле. Для составления уравнения такого нелинейного звена удобно, как

всегда, ввести отклонения A/g и Дг от некоторых постоянных значений 1\ и Л . Как указано на рис. 16.17, а, принимаем

1 + -Ср

(16.35)

Тогда характеристика данного нелинейного звена в отклонениях примет вид рис. 16.17, б, симметричный относительно начала координат (релейная характеристика с гистерезисной петлей).

В связи с этим уравнение нелинейного звена (рис. 16.17, б) будет

Дг = Ti sign (Д/а - ti) при Дг = Г1 sign (Д/з + ii) при

dh dt

>0, <0,

(16.36) (16.37)

где выражение sign (AI - н) обозначает знак величины (АТ - ц). Формулы (16.36) и (16.37) отвечают соответственно движению вправо по линии ABCEF (рис. 16.17) и влево по линии FEDBA, причем в точках С mD происходит переключение реле (перескоки в точки Е ш В соответственно).

Уравнения линейной части системы (16.33) и (16.34), имея в виду исследовать переходный процесс при / (f) - О, объединим в одно:

{Тр + 1) {Тр + 1) Ah = ~1фАг.

(16.38)

Постоянные значения, от которых производится здесь отсчет отклонений переменных, определяются из алгебраических уравнений условного номинального установившегося режима

f/ = (i?i + ri)i, (i?2+i? )/ = C/ , 11 =

+ /ср

с использованием реальных характеристик генератора.

Система автоматического регулирования курса водяной торпеды. Возьмем описанную в § 1.3 простейшую схему (рис. 1.20). Уравнение вращения торпеды вокруг вертикальной оси (рыскание по курсу) как регулируемого объекта запишем приближенно в виде

4- = -сф, (16.39)

где ij; - угол отклонения торпеды от заданного направления, / - ее момент инерции относительно вертика.пьной оси, сф - момент сопротивления среды

(воды), - момент руля, б - угол поворота руля. Разделив (16.39) на Cj, получим уравнение регулируемого объекта в виде

(16.40)

Чувствительным элементом является трехстепенный гироскоп, поворачивающий рычаг заслонки в системе питания пневматической рулевой

Рис. 16.18.

машинки на угол, пропорциональный углу отклонения торпеды. Следовательно, уравнение чувствительного элемента будет

S = к., (16.41)

где S - величина перемещения заслонки из нейтрального положения.

Будем считать, что поршень рулевой машинки 3 (рис. 1.20) при открытии заслонки, быстро получая полную скорость, мгновенно ) перебрасывает руль из одного крайнего положения в другое.

Б таком приближенном представлении лпнейная часть системы ограничивается уравнениями (16.40) и (16.41). Единое уравнение линейной части системы поэтому будет

{Т + 1) ps = -кфф. (16.42)

Рулевая машинка вместе с рулем (привод и регулирующий орган) представляет собой нелинейное звено, уравнение которого согласно вышесказанному моншо представить либо в простейшем виде (рис. 16.18, я)

б = с sing S, (16.43)

либо, если имеется заметная зона нечувствительности (рис. 16.18, б), в виде

6 = 0 при -b<;s<;-rb,

< . . [ (16.44)

6 = csigns при s>o, J

либо, если существенное значение имеет гистерезисная петля (рис. 16.18, б),

(16.45)

.иибо, наконец, в простейшем случае, но с запаздыванием (рис. 16.18, г)

} (16.46)

6 = csign(s-Ъ) при ps>-0, б = с sign (s-Ь Ь) при ps<:0,

6 = .csign(s-st;) при ps>0,

б = с sign (s-1-I St; I) при ps<:0.

1) Точнее, за такое малое время, в течение которого торпеда не успевает заметно повернуться, т. е. много меньшее возможного периода колебаний торпеды.

S, S (т), (16.47)

причем т - время запаздывания срабатывания реле.

При исследовании системы в целом можно принять один из этих четырех вариантов в зависимости от того, какой из них лучше будет соответствовать свойствам данной релейной системы.

§ 16.3. Уравнения систем с нелинейностью в виде сухого трения и зазора

Приведем примеры составления уравнений для нелинейных систем с сухим трением или зазором в механической передаче.

Следящая система с линейным и сухим трением. В § 5.7 составлены уравнения следящей системы в линейном виде. Рассмотрим теперь такой случай, когда к линейному моменту трения Мт добавляется еще момент сухого трения Меч, имеющий постоянную величину, равную некоторому значению с, и меняющий свое направление (знак) с изменением знака скорости вращения объекта (рис. 16.19). Следовательно, теперь уравнение управляемого объекта примет вид

= Мвр - - Мч, ЛГвр = cii , = срр, (16.48)

где р - зтол поворота вала управляемого объекта, причем

McT = csignpP при рфО,\

-сМеч< + с при рр = 0. j (1-

Важная особенность сухого трения состоит в том, что это (в отличие от релейных характеристик) далеко не всегда означает мгновенное переключение величины Мс1 при рр = 0. N/fcr - Здесь возможны два варианта: 1) рр = О и I Мвр I > с,

-Pfi-brPfi 2) рр = О и I Мвр К с.

(16.50)

В первом случае скорость объекта рр пройдет через нулевое значение и его движение будет продолжаться, без остановки дальше по закону (16.48). Во втором же случае произойдет остановка управляемого объекта, в течение которой будет иметь место не переключение, а медленное изменение величины AfcT в интервале -с Мст + с (или обратно), причем Мст будет принимать все время определенные значения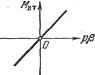

Мс, = Мвр (рр = о, I Мвр I < с).

(16.51)

В этом случае движение возобновится снова только тогда, когда вращающий момент достигнет значения Мвр = с и превысит его.

Если же остается Мвр < с, то система будет неподвижна. Поэтому положение равновесия управляемого объекта оказывается неопределенным внутри некоторого отрезка, а именно при любом значении Мвр < с. Этим определяется зона застоя системы. Застой проявляется в том, что, с одной стороны, система не будет двигаться при изменении угла задатчика в определенном интервале и, с другой стороны, что система будет обладать ошибкой из-за сухого трения в положении равновесия. В процессе же движения системы в одну сторону с любой скоростью сухое трение внесет постоян-