На рис. 16.11, а показаны два возможных варианта (кривые 1 ш 2) протекания такого процесса. Легко видеть, что на фазовой плоскости (ж, у)

это изобразится кривыми ffpj; 1 ш 2 соответственно

(рис. 16.11, б), так как в первом варианте все время ж > О и z/ < О, а во втором варианте знаки х шу меняются по одному разу. Границы областей 1 и 2 представляют собой прямые у = -ах и у=-ах, получающиеся из уравнений (16.27) соответственно при ttg = О и при = О (обращение одного из корней в нуль).

В отличие от прежнего здесь все фазовые траектории вливаются непосредственно в начало координат О фазовой плоскости. Однако изображающая точка М не попадает в начало координат в конечное время, а приближается асимптотически.

Итак, затухающим апериодическим процессам в системе отвечают фазовые траектории, вливающиеся в начало координат.

Случай 5. Этот случай (вещественные положительные корни) соответствует также апериодическому процессу, определяемому теми же уравнениями (16.27), но при tt] < О Е 2 < 0. Аналогично предыдущему получаем кривые процесса и фазовые траектории, изображенные на рис. 16.12.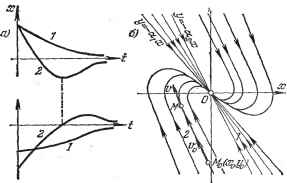

Рис. 16.11.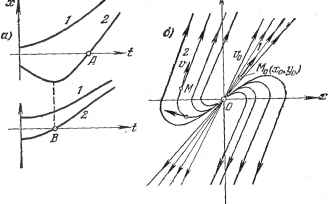

Рис. 16.12.

Случай 6. В этом случае (вещественные корни разных знаков) также имеет место апериодический процесс (16.27) (рис. 16.13, а), гдеа и имеют разные знаки, но картина фазовых траекторий здесь иная. Так как <; О, то введем обозначение а® = -а, причем для простоты построений рас-

§ 16.1]

ОБЩИЕ ПОНЯТИЯ!

смотрим случай = О, что соответствует согласно (16.23) уравнению системы - ах = О и согласно (16.25) - уравнению фазовых траекторий

(16.28)

= 1,

Интегрирование последних, аналогично случаю 1, дает - (С)

т. е. семейство гипербол, изображенное на рис. 16.13, б.

Направления движения изображающей точки М по фазовым траекториям, показанные на рис. 16.13, б, легко определяются в каждой четверти ПЛОСКОСТИ ПО знаку dyldx (16.28).

Аналогичная картина фазовых траекторий получится в данном случае и при аф{).

Итак, расходящимся апериодическим процессам в системе отвечают фазовые траектории типа рис. 16.12, б или типа рис. 16.13, б, причем

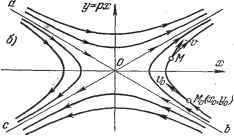Рис. 16.13.

изображающая точка, двигаясь по ним, в конечном итоге удаляется от начала координат.

Особые точки. В точках, которые соответствуют установившемуся состоянию, получаем согласно (16.25) неопределенное выражение

= - 1 -йг-д

т. е. неопределенное направление касательных к интегральньш кривым (фазовым траекториям). Такие точки называются особьши точками, причем существует следующая классификация для них:

а) особые точки типа точки О на рис. 16.8, б называются центрами,

б) особые точки типа рис. 16.9, б называются устойчивыми фокусами,

в) особые точки типа рис. 16.10, б называются неустойчивыми фокусами,

г) особые точки типа рис. 16.11, б называются устойчивыми узлами,

д) особые точки Т1ша рис. 16.12, б называются неустойчивьши узлами,

е) особые точки типа рис. 16.13, б называются седлами (седло всегда неустойчиво).

Особые линии для нелинейных систем. Реальные системы автоматического регулирования можно считать линейными чаще всего в предположении малости отклонений переменных от их значений в определенном установившемся состоянии.

За пределами указанной области вследствие значительного отклонения характеристик от линейных картина фазовых траекторий может сильно измениться и стать качественно иной.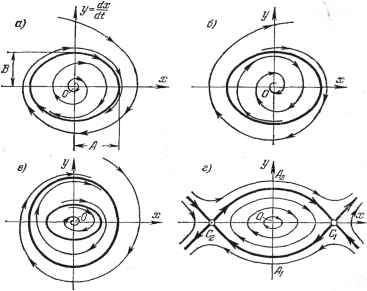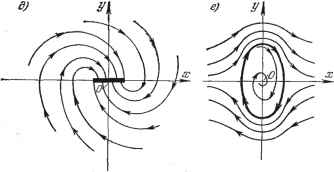

Рис. 16.14.

линейная автоматическая система как бы превращается в устойчивую нелинейную автоколебательную систему (система генерирует устойчивые ко-.пебания определешюй формы).

Картина фазовых траекторий для такой системы изображена на рис. 16.14, а. Здесь вблизи начала координат получаются спирали, как в неустойчивой линейной системе (рис. 16.10, б), но далее все они расходятся не до бесконечности, а приближаются асимптотически к некоторому замкнутому контуру ограниченных размеров, как показано на рис. 16.14, а. К нему же приближаются и все спирали, находящиеся вне контура. Это

В частности, если по линейной теории система оказывается неустойчивой и процесс начинает расходиться, то может оказаться, что из-за фактической нелинейности характеристик он не будет расходящимся неограниченно. Амплитуда расходящихся колебаний может увеличиваться только до определенного значения, а затем оставаться постоянной, т. е. неустойчивая