величины У = -jT . Тогда уравнение системы (16.23) преобразуется к виду

) (16.24)

увеличении времени. Фазовые траектории неустойчивой линейной системы будут неограниченно удаляться от начала координат.

Для нелинейной системы вследствие ряда особенностей процессов, отмечавшихся выше, фазовые траектории могут принимать самые разнообразные очертания. Если имеется асимптотическая устойчивость для определенного круга начальных условий, то все фазовые траектории, которые начинаются внутри определенной области т), окружающей начало координат фазового пространства (рис. 16.7, б), будут асимптотически приближаться к началу координат. Если устойчивость неасимптотическая, то фазовые траектории, начинающиеся внутри определенной области т) вокруг начала координат фазового пространства, могут иметь любые очертания, но не будут выходить за пределы некоторой определенной области е, окружающей начало координат (рис. 16.7, б).

Формулировка понятия устойчивости по Ляпунову. Невозмущенное движение (установившийся процесс) называется устойчивым, если при заданной сколь угодно малой области е (рис. 16.7, б) можно найти такую область т), что при начальных условиях, расположенных внутри этой области, возмущенное движение (переходный процесс) будет таким, что изображающая точка не выйдет из области е при любом сколь угодно большом значении времени t.

В аналитической записи формулировка понятия устойчивости по Ляпунову будет следующей. Невозмущенное движение (установившийся процесс) будет устойчивым, если при заданных положительных сколь угодно малых числах 8j можно найти такие положительные числа т) (г = 1, . . ., п), что при начальных условиях

lioK-m (f = 1, п) (16.22)

решение дифференциальных уравнений возмущенного движения (переходного процесса) удовлетворяет неравенствам

\xi {t) К 8г (i = 1, . . ., тг)

при любом сколь угодно большом t, начиная с некоторого t = Г > 0.

Представим себе для этой аналитической записи геометрический образ в фазовом пространстве.! Очевидно, что при ограничении начальных условий по каждой координате неравенствами (16.22) получается тг-мерный параллелепипед со сторонами 2t)j, внутри которого должна лежать начальная точка фазовой траектории (жю, хо, . . ., хо). На фазовой плоскости (тг = 2) он обращается в прямоугольник. Аналогично и второе из написанных неравенств геометрически означает, что фазовые траектории не должны выходить из параллелепипеда со сторонами 28£.

В формулировке Ляпунова содержится требование сколь угодной малости указанных областей. Однако практически это определение, так же как и теоремы Ляпунова, которые будут приведены ниже, применяется и тогда, когда эти области имеют определенные конечные размеры.

Фазовые траектории для обыкновенных линейных систем. Пусть переходный процесс в некоторой системе описывается уравнением второго порядка

+ а, + ах=.0. (16.23)

Введем обозначение для скорости изменения отклонения регулируемой dx Tt

Исключим из уравнений (16.24) время t, разделив первое из них на второе (при ж и j/ =50):]

= - 1 - -.

(16.25)

Решение z/ = ф (ж) этого дифференциального уравнения с одной произвольной постоянной определяет собой некоторое семейство так называемых интегральных кривых на фазовой плоскости (ж, у), каждая из которых соответствует одному определенному значению произвольной постоянной.

Вся совокупность интегральных кривых представит собой все возможные фазовые траектории, а значит, и все возможные виды переходного процесса в данно!! системе автоматического регулирования при любых начальных условиях.

Рассмотрим отдельно различные случаи. Уравнению (16.23) соответствуют корни характеристического уравнения

1 ,

Pi, 2 = - -9- ±

причем возмолшы шесть случаев:

1) корни чисто мнимые при = О, > О (граница устойчивости линейной системы);

2) корни комплексные и имеют отрицательные вещественные части при а\ <z 42, > О, > О (устойчивая линейная система);

3) корни комплексные и имеют положительные вещественные части при al <; 42, их <; О, 2 > О (неустойчивая линейная система);

4) корни веществехшые отрицательные при > 42, >- О, (устойчивая линейная система);

5) корни вещественные положител[ьные при al > 42, < О, 2 > О (неустойчивая линейная система);

6) корни вещественные и имеют разные знаки при а<0 (неустойчивая линейная система); в частности, один из корней будет равен нулю при 2 = 0 (граница устойчивости линейной системы).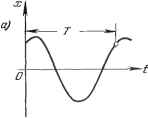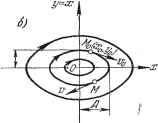

Рис. 16.8.

Случай 1. В первом случае получаются, как известно, незатухающие колебания (рис. 16.8, а)

x = Asm{(ot + ), z/ = - = o)co.s(o)i + p), o) = l/, (16.26)

с постоянной амплитудой А и начальной фазой р, которые зависят от начальных условий. Для фазовой плоскости уравнения (16.26) представляют собой параметрические уравнения эллипса с полуосями А и аА (рис. 16.8, б). Уравнение эллипса

можно получить непосредственньш решением дифференциального уравнения фазовых траекторий (16.25) при = О и = о), причем А - произвольная постоянная интегрирования.

Итак, периодическим колебаниям системы (рис. 16.8, а) соответствует движение изображающей точки по замкнутой кшвой (рис. 16.8, б).

Случай 2. В этом случае (комплексные корни с отрицательньши вещественньши частями), как известно, имеют место затухающие колебания (рис. 16.9, а)

X = Ле- *sin (o)i -]- Р), z/ = - = уАе- - cos (cof + Р + б).

а произвольные постоянные Лир определяются из начальных условий:

У = Уо = при t = 0.

Значения ж и z/ не возвращаются за период колебания к прежним, а становятся меньше. Это дает на фазовой плоскости (ж, у) кривую (рис. 16.9, б),

S) ра: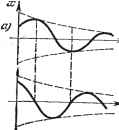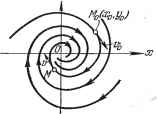

Рис. 16.9.

которая за один оборот не возвращается в прежнюю точку М-, а подходит ближе к началу координат.

Итак, затухающим колебаниям системы (рис. 16.9, а) отвечают фазовые траектории в виде спиралей, по которьш изображающая точка приближается к началу координат (рис. 16.9, б).

Случай 3. Этот случай (комплексные корни с пололительными вещественными частями) соответствует расходящимся колебаниям (рис. 16.10, а). Рассуждая аналогично предыдущему, получим всю совокупность возможных фазовых траекторий тоже в виде спиралей, но только

изображающая точка будет двигаться по ним не к началу координат, а от него (рис. 16.10, б).

Случай 4. Этот случай (вещественные отрицательные корни) соответствует апериодическому процессу

= Cie- i4C2e- 2t, y = ajCie- i -ct,C2e- 2t, (16.27)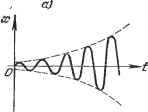

Рис. 16.10.