а на участке BD

Решение уравнения (16.12) будет

(16.13)

(16.14)

откуда получаем

е = -ГАе -kict + C.

(16.15)

Условимся для простоты отсчитывать время t от начала участка АВ (рис. 16.5, а). Тогда начальные условия будут

где пока неизвестно. Используя начальные условия, находим произвольные постоянные для уравнения (16.15):

Ci = + кгс с = ъ + TCi.

(16.16)

Аналогично для участка BD согласно (16.13), отсчитывая время t тоже от начала этого участка (рис. 16.5, б), получим решение

dQ dt

= С[е +к,с, t

6= -TiC[e +hct + C, C = %-hc, C,= ~b+T,C[. }

(16.17)

Bee остальные участки кривой переходного процесса будут определяться, очевидно, такими же решениями, но только с другими числовыми

значениями величин С, Cg, 9а, С[, С, G. Заметим, что величины G. и б,. необходимые для определения произвольных постоянных, находятся как

значения G в конце предшествующих им участков. Поэтому, если будет

задана величина 6 в начальной точке первого участка процесса, то все вышенаписанное решение для переходного процесса в системе станет определенным. Такой метод решения задачи называется методом припасовыва-ния.

Выясним теперь, возможны ли в данной системе автоколебания, т. е. устойчивое периодическое решение. Для этого нужно, очевидно, чтобы в конце/) одного периода колебаний (рис. 16.4, б) получились точно такие Лхе

значения 6 и G, какие были в начале его А. Легко заметить, что при этом оба полупериода {АВ и BD) должны быть одинаковыми вследствие симметрии характеристики (рис. 16.4, с). Поэтому для определения автоколебаний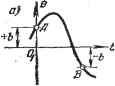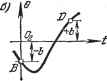

Рис. 16.5.

достаточно рассмотреть только один участок АВ и потребовать, чтобы

ё=-ёл. (16.18)

Обозначив период искомых автоколебаний через 2Т, а длительность участка АВ, следовательно, через Т, из (16.14) найдем

Подставляя сюда (16.18) и замечая, что из (16.16) = - kiC, получаем выражение

Ci(l+e ri)=2/cic.

(16.19)

в котором содержатся две неизвестные: Ci и Т. Величину Т (длительность, участка АВ) можно выразить из (16.15), так как известно, что в конце участка 6 = -6. Из (16.15) и (16.16) при этом находим

riCi(l -е ri) - kicT~2b.

Подставив сюда значение Ci из (16.19), получим уравнение для определения полупериода автоколебаний:

2Ti 2Ti kicTi

(16.20)

Это трансцендентное уравнение для Т легко решается графически (рис. 16.6) пересечением двух кривых:

Г Г ъ

Если найдено вещественное положительное значение для Г, то это свиде- Рис. 16.6. тельствует о наличии периодического решения в даннойсистеме. Чтобы доказать, что это соответствует автоколебаниям, нужно исследовать их устойчивость, т. е. показать, что в переходном процессе система ведет себя, как изображено на рис. 16.3, с, но не так, как на рис. 16.3, б. Это будет показано ниже.

Амплитуда найденных автоколебаний определяется как Эщах на участке АВ (рис. 16.5, с) путем исследования функции (16.15) на максимум обычным путем.

Фазовое пространство. Для наглядного представления о сложных нелинейных процессах регулирования часто прибегают к понятию фазового пространства, которое заключается в следующем. Дифференциальное уравнение замкнутой системы регулирования тг-го порядка можно преобразовать к системе п дифференциальных уравнений первого порядка в виде

r = Oi{xi, Xz, Хп, f,g).

= OziXi, Xz, ...,Xn,f, g),

dx ~di

P = On{0Ci, Xz, Xn, f,g)

(16.21)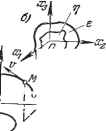

<с начальными условиями

1 = *10. 2 = аго. ; - по при t = о,

где х, х, . . ., Xji - переменные, являющиеся искомыми функциями времени, причем х может обозначать регулируемую величину, з. х, . . х - вспомогательные переменные; fug - возмущающее и задающее воздействия.

Пусть, например, в уравнениях (16.21) будет п = 3 (система третьего порядка). Переменные ж, х, Xg здесь могут иметь любой физический смысл.

Но условно их можно представить мысленно как прямоугольные координаты некоторой точки М (рис. 16.7, с).

В реальном процессе регулирования в каж-aj Ч J Дый момент времени величины х, х, Хд имеют

-- вполне определенные значения. Это соответствует

тч вполне определенному положению точки М в

f I \Мо(1-о) пространстве (рис. 16.7, с). С течением времени

--! у * В реальном процессе величины Ж], х, х опреде-

ленным образом изменяются. Это соответствует щ определенному перемещению точки М в простран-

стве по определенной траектории. Следовательно, Рис. 16.7. траектория движения точки М может служить

наглядной геометрической иллюстрацией динамического поведения системы в процессе регулирования.

Точка М называется изображающей точкой, ее траектория называется фазовой траекторией, а пространство (х, х, х называется фазовым пространством.

Так как производные по времени от координат точки представляют проекции ее скорости v на оси координат, то дифференциальные уравнения системы в форме (16.21) представляют собой выражения для проекций скорости V изображающей точки М (рис. 16.7, с) на оси координат. Следовательно, по значениям правых частей уравнений (16.21) в каждый момент времени моншо судить о направлении движения изображающей точки М, а вместе с тем и о поведении соответствующей реальной системы в процессе регулирования.

Начальные условия процесса регулирования (ж, х, х) определяют координаты начальной точки фазовой траектории (рис. 16.7, с).

Если переменных в уравнениях (16.21) будет всего две: х- и х (система второго порядка), то изображающая точка будет двигаться не в пространстве, а на плоскости {фазовая плоскость).

Если переменных будет любое число тг > 3 (система тг-го порядка), то фазовое пространство будет не трехмерным, а тг-мерным.

Итак, фазовое пространство и фазовые траектории представляют собой лишь геометрический образ динамических процессов, протекающих в системе. В этом геометрическом представлении участвуют координаты и исключено время. Фазовая траектория сама по себе дает лишь качественное представление о характере поведения системы. Чтобы определить количественно положение изображающей точки (а значит, и состояние системы) в любой момент времени, нужно найти решение заданных дифференциальных уравнений (16.21) во времени.

Если уравнения (16.21) составлены в отклонениях от установившегося состояния, то последнее характеризуется значениями ж = 2 = . . . =а; =0. Следовательно, изображением установившегося состояния системы является начало координат фазового пространства.

Отсюда вытекает, что фазовые траектории устойчивой линейной системы будут асимптотически приблшкаться к началу координат при неограниченном