§ 16.1]

ОБЩИЕ ПОНЯТИЯ

мер, система на рис. 16.2, с, если в ее уравнениях под знаками нелинейных функций находятся входные (или выходные) величины обоих нелинейных звеньев, и многие другие системы.

Системы с логическими устройствами относятся обычно к нелинейным системам второго класса.

Заметим, что во всех случаях, когда под знак нелинейной функции входит какая-либо линейная комбинация разных переменных, их следует

\ Линейная чаешь JV

Линейная часплл

\Нелиней- jz Нелиней-ное звено! оезвено!1\\

Линейная vacma систет/

Рис. 16.2.

обозначать одной буквой, а данную линейную комбинацию учесть при составлении общего уравнения линейной части системы. Это бывает, например, в тех случаях, когда на вход нелинейного звена подаются производные или включается обратная связь. Так, если для рис. 16.1, б

то, обозначая

Xz = F (zi -Ь A;ipzi - kz, -- kpz. - kz ~

(16.6)

можно привести уравнение нелинейного звена к виду (16.1).

Из всех уравнений линейных звеньев, а также добавочных линейных выражений типа (16.6), получаемых при выделении нелинейности, составляется общее уравнение линейной части системы

Q (р) X, = -R (р) X, (16.7)

(где Q (р) в. R (р) - операторные многочлены) или передаточная функция линейной части системы

R{p)

Wip)-

QiP)

Составление уравнений будет проиллюстрировано ниже на примерах.

(16.8)-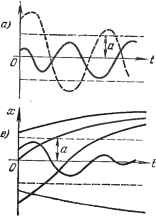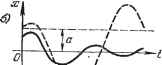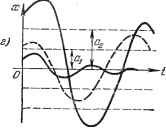

------

Рис. 16.3.

возникают автоколебания, то установившееся состояние, соответствующее-постоянному значению регулируемой величины, часто становится невоз-можньш.

Следовательно, в общем случае на плоскости параметров системы могут быть не два вида областей (устойчивости и неустойчивости), как в линейных системах, а больше: 1) область устойчивости равновесного состояния с постоянньш значением регулируемой величины; 2) область устойчивых автоколебаний; 3) область неустойчивости системы; 4) области, соответ-ствуювзде другим, более сложным случаям.

Если процессы в системе имеют вид, указанный на рис. 16.3, , то равновесное состояние (х = 0) неустойчиво. В том случае, когда оба указанных на рис. 16.3, с колебания в переходных процессах стремятся к одной и той же амплитуде и к одной и той же частоте, система будет обладать устойчивыми автоколебаниями с амплитудой с.

На рис. 16.3, бив показаны случаи, когда равновесное состояние {х = 0) системы устойчиво в малом , т. е. при начальных условиях, не выводящих отклонения в переходном процессе за определенную величину с, и неустойчиво в большом , т. е. при начальных условиях, выводящих отклонение в переходном процессе за пределы величины с. Здесь граничным процессом является неустойчивый периодический процесс собственного движения системы с амплитудой а (переходные процессы расходятся от него в обе стороны).

На рис. 16.3, г показан случай трех возможных установившихся состояний: 1) равновесное состояние (х - 0), 2) колебания с постоянной амплитудой 1, 3) колебания с постоянной амплитудой а. При этом колебания с амплитудой Cj неустойчивы. В результате система будет устойчива в малом*

Процессы в нелинейных системах автоматического регулирования имеют целый ряд весьма существенных особенностей, которые не встречаются в линейных системах.

Благодаря этим существенным особенностям даже вопрос об устойчивости системы становится здесь более сложным Кроме структуры системы и значений ее параметров для устойчивости того или иного установившегося процесса имеют значение здесь, в отличие от линейных систем, также и начальные условия. Возможен новый вид установившегося процесса - автоколебания, т. е. устойчивые собственные колебания с постоянной амплитудой при отсутствии внешних колебательных воздействий. Когда в системе

по отпошепию к равновесному состоянию а; = О, а в большом система -будет обладать устойчивыми автоколебаниями с амплитудой Cj.

Пример. Для иллюстрации особенностей нелинейной системы исследуем переходный процесс и автоколебания в релейной системе автоматического регулирования температуры, изображенной на рис. 1.35. Для этого составим сначала уравнения регулируемого объекта и регулятора.

Пусть регулируемый объект представляет собой некоторую камеру. Учитывая инерционность процесса нагрева в охлаждения, запишем уравнение регулируемого объекта в виде

(16.9)

где е - отклонение температуры, ф - отклонение регулирующего органа, / (t) - внешние возмущения.

При отклонении температуры 6 появляется ток в диагонали моста того или иного направления (рис. 1.35) и замыкается тот или иной контакт реле, включающего постоянное напряжение в ту или иную обмотку возбуждения электродвигателя. Приняв во внимание некоторое отставание в этом процессе включения, получим релейную характеристику вида г) рис. 1.36. Далее, считая, что ток /пропорционален отклонению температуры объекта 6,

а скорость отклонения регулирующего органа пропорциональна напряжению на обмотках возбуждения электродвигателя, можно в дайном случае выходной величиной для указанной релейной характеристики считать

прямо , а входной - 6 (рис. 16.4, а).

Следовательно, уравнение регулятора образом: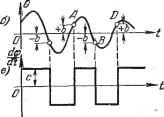

Рис. 16.4.

запишется здесь следующим

когда

когда

>0;

<0.

(1,6.10)

(16.11)

Рассмотрим два произвольных участка переходного процесса (при / (t) = 0) в данной системе (участки АВ и BD на рис. 16.4, б).

На участке АВ уравнение регулятора согласно рис. 16.4, в будет

~ = +с. Дифференцируя (16.9) по t ж подставляя туда + с, получаем

при /(0 = 0 следующее уравнение системы регулирования на участке АВ:

(16.12)