Дискретная передаточная функция

(15.155)

где d = е /1. Сделаем подстановку z = e-*® = cos соГ + / sin со Г. В результате получим

Г vfc(cos(o?4-/sin(or) созсоУ-d-]-]sin ч)Т

(15.156)

Модуль и аргумент этого выражения

Ж(е =

smcoT

ф = arg Ж (eJ ?) =(йТ~ arctg

coscoT-d

(15.157)

Аналогичным образом могут быть найдены частотные передаточные функции замкнутых систем Ф (z) и Ф (z) при z = e® .

§ 15.4. Устойчивость и качество импульсньпс систем регулирования

В импульсных системах автоматического регулирования устойчивость будет иметь место, если все полюсы передаточной функции замкнутой системы, т. е. корни характеристического уравнения, лежат в левой полуплоскости корней. Границей устойчивости является мнимая ось (рис. 15.16, а). Для

Л 1т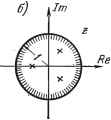

Рис. 15.16.

построения области устойчивости в плоскости комплексной величины z отобразим мнимую ось плоскости величины р на плоскость z. Для этой цели в соответствии с методом 1)-разбиения необходимо сделать подстановку р = ш менять затем частоту со в пределах от -оо до -j-oo. Таким образом, получаем z = е = е*.

При изменении частот в указанных пределах на плоскости z получится окружность единичного радиуса, представляющая собой область устойчивости (рис. 15.16, б).

Условием устойчивости будет нахождение особых точек (полюсов) передаточной функции замкнутой системы Ф (z) внутри этой окружности. Следовательно, корни характеристического уравнения

1 -Н (z) = О (15.158)

должны быть ограничены по модулю: Zj- <С 1, что совпадает с результатом §15.1.

Так, nanpmviep, для характеристического уравнения первого порядка

Z + А = 0 (15.159)

очевидное условие устойчивости будет \ А < 1-

(15.161)

Аналогичным образом можно показать, что для уравнения второго порядка

z + Az + B = 0 (15.160)

путем вычисления его корней получаются три условия устойчивости:

1 + А + В>0, 1-А+В>0, 5<1.

Для уравнений более высокого порядка исследование устойчивости усложняется. Для облегчения задачи иногда используется так называемое w-преобразование, посредством которого окружность единичного радиуса (рис. 15.16, б) отображается на мнимую ось плоскости комплексной величины W. Для преобразования используется подстановка

=4S- . . 5-162)

или, соответственно,

w = . (15.163)

Сделав подстановку z = e , получаем из (15.163)

где Х ~ \g~- представляет собой так называемую относительную псевдочастоту. Иногда вводится в рассмотрение абсолютная псеедочастота

X = -tg- = .. (15.165)

При малых частотах tg Y псевдочастота Я со. Поэтому при

выполнении условия соГ < 2 можно заменить в расчетах псевдочастоту действительной частотой, что может быть использовано, в частности, при расчетах установившихся ошибок при гармоническом входном сигнале.

Нетрудно видеть, что при изменении частоты в пределах - со

псевдочастота пробегает все значения от - оо до -f-oo, комплексная величина W движется по оси мнимых от -/оо до /оо. Областью устойчивости в этом случае оказывается вся левая полуплоскость (рис. 15.16, в). Поэтому для передаточной функции с г/;-преобразованием могут использоваться обычные критерии устойчивости, справедливые для непрерывных систем.

Рассмотрим, например, характеристическое уравнение второго порядка (15.160). Посредством подстановки (15.162) оно преобразуется к виду

{\ - А В) + 2 (1 - В) W + i + А + В ~ (15.166)

На основании алгебраического критерия (см. § 6.2) условие устойчивости для уравнения второго порядка сводится к требованию положительности всех коэффициентов. Отсюда получаются условия (15.161).

Заметим также, что применение г/;-преобразования и псевдочастоты Я приводит передаточную функцию разомкнутой системы к виду, удобному для использования метода логарифмических частотных характеристик.

Для определения устойчивости замкнутой импульсной системы возможно использование критерия Найквиста. Для этой цели можно пршюнять передаточную функцию разомкнутой системы, полученную как на основе z-преобразования, так и на основе гг;-преобразования. И в том и в другом случае

амплитудно-фазовая характеристика разомкнутой системы не должна охва-тьшать точку (-1, /0). При использовании передаточной функции W {z) амплитудно-фазовая характеристика становится периодической функцией с периодом 2пТ~.

Пусть, например, дискретная передаточная функция разомкнутой системы имеет вид

W{z) = -. (15.167)

Получим частотную передаточную функцию подстановкой z == е®:

(-- )- coscor-fl;sin.r - --/ctg =u + jv. (15.168)

Б координатах и = Re W ж v = Im W амплитудно-фазовая характеристика будет представлять собой вертикальную прямую линию, отстоящую влево от начала координат на величину 0,5 КТ. Гранща устойчивости будет при прохождении этой прямой через точку (-1, /0). Отсюда можно получить условие устойчивости КТ < 2.

Получим теперь частотную передаточную функцию на основе 1г;-пре-образования. Для этого в формуле (15.167) применим подстановку (15.162). В результате, получш! передаточную функцию разомкнутой системы как функцию комплексной величины w:

*) = Ц, (15.169)

Частотная передаточная функция разомкнутой системы при подста-Т

новке W =

W*[i-Ll>l= 2 . (15.170)

Нетрудно видеть, что частотная передаточная функция (15.170) в зависимости от псевдочастоты имеет более простой вид по сравнению с (15.169). По выражению (15.170) может быть, в частности, просто построена асимптотическая л. а. X.

Подобным же образом могут быть получены дискретные передаточные функции Ф* (w) и Ф* (w), а также частотные передаточные функции Ф* (уу)

Оценка качества импульсной системы регулирования может делаться построением кривой переходного процесса, что при использовании z-преобразования осуществляется сравнительно легко (§ 15.2), а также посредством различных критериев качества. Наиболее простым является использование показателя колебательности, который может характеризовать запас устойчивости системы. Как и в случае непрерывных систем, получение заданного показателя колебательности сводится к требованию, чтобы амплитудно-фазовая характеристика системы не заходила в запретную зону, окружающую точку (-1, /0) в соответствии с рис. 8.27.

Установившаяся точность импульсной системы может оцениваться по коэффициентам ошибок. Аналогично непрерывным системам, начиная с некоторого момента времени ошибку импульсной системы регулирования можно представить в виде ряда

x[n] = Cogln] + c,iln] + g[n]i-..., . (15.171)