РАЗДЕЛ II

ОБЫКНОВЕННЫЕ ЛИНЕЙНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ

ГЛАВА 3

ЛИНЕАРИЗАЦИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ

§ 3.1. Линеаризация уравнений

При составлении дифференциальных уравнений динамики любой автоматической системы последнюю разбивают на отдельные звенья и записывают уравнение каждого звена в отдельности. Уравнения всех звеньев образуют единую систему, которую можно преобразовать к одному уравнению путем исключения промежуточных переменных.

Уравнение звена должно быть составлено так, чтобы оно выражало зависимость (в динамическом процессе) между теми величинами, которые в схеме исследуемой системы ука-

Звено

Рис. 3.1.

заны на выходе и входе данного звена, т. е. между величинами, представляющими воздействие данного звена на последующее по схеме звено и воздействие предыдущего звена на данное. Динамическое уравнение отдельного звена составляется по правилам соответствующей технической науки (звено может представлять собой тепловой двигатель, электрическую машину, механическую передачу, электрическую цепь, ламповую схему и т. п.).

Звено может иметь иногда не одну входную величину, а несколько (например, при наличии дополнительных обратных связей). Кроме входной и выходной величин звена, которые выражают собой внутренние связи между звеньями данной системы, может учитываться также внешнее воздействие.

Пусть, например, звено (рис. 3.1, а) какой-нибудь автоматической системы имеет входные величины ж, х, выходную - Жд и внешнее воздействие /, а динамическое уравнение звена имеет произвольный нелинейный вид

F {Х, Xt Ж2, Жд, Жд, Жд, Жд) - (f (/, /)

(3.1)

(для примера взят определенный порядок входящих в уравнение производных Ж2, Жд,./; вообще же здесь могут быть любые другие варианты).

Допустим, что установившийся процесс в системе имеет место при некоторых постоянных значениях ж = х\, = ж, Жд = ж и / = Тогда уравнение установившегося состояния для данного звена согласно (3.1) будет

F (ж5, ж , О, ж . О, О, 0) = ф (/ , 0).

(3.2)

Xi{t) = x\ + Kxi{t) xг{t) = xl + xг{t)

, Xz (t) = .rg + Axz (t), X2 = Ax2, \

- ...........f (3.3);

), Xz==Ax3, X3 = Axs, Xs = Ax3. )

Условие достаточной малости динамических отклонений переменных от некоторых установившихся значений для системы автоматического регулирования и следивших систем обычно выполняется. Этого требует сама идея работы, замкнутой автоматической системы.

Внешнее же воздействие / не зависит от работы автоматической системы изменение его может быть произвольным, и поэтому правая часть уравнения (3.1) обычно линеаризации не подлежит (в отдельных случаях и она; может быть линеаризована).

Первый способ линеаризации. Разложим функцию F, стоящую в левой; части уравнения (3.1), в ряд по степеням указанных выше малых отклонений, рассматривая все производные тоже как самостоятельные переменные. Тогда уравнение (3.1) примет вид

F{A, А. О, х% О, О, 0)+(-)°Дх,-ь(-)° Дх,-ь(-)°Дх,+

з / \ tog / 3 dxs

+ (члены высшегопорядка малости) = ф (/, /), (3.4)

где через для краткости обозначена неличина взятая при х = х\,.

х = х1, Ж2 = О, Жд = а*, . . ., Жд = О (т. е. сперва берется в общем виде частная производная от функции F по х, после чего в нее вместо всех переменных подставляются их постоянные значения х\, х% О, х, . . ., 0).

Следовательно, все частные производные в полученном уравнении (3.4) представляют собой некоторые постоянные коэффициенты. Они будут переменными во времени, если функция F содержит t в явном виде или если установившийся процесс- в системе определяется переменными значениями-х1 it), xl it), 4 it).

Члены высшего порядка малости, указанные в уравнении (3.4), состоят из произведений и степеней малых отклонений Дж, Ах, ... с коэффициентами в виде смешанных частных производных и частных производных второго-и высших порядков от функции F по всем переменным.

Вьгатя из уравнения (3.4) почленно уравнение установившегося состояния (3.2) и отбросив члены высшего порядка малости, получим искомое линеаризованное уравнение динамики данного звена в виде

+ дз + ( )<дУз + (-)д;=Ф(/, /)-Ф(Л 0). (3.5)

В основе линеаризации нелинейных уравнений лежит предположение о том, что в исследуемом динамическом процессе переменные (в данном случае Xj, Х2, Жд) изменяются так, что их отклонения от установившихся значений {з1, х1, ж) остаются все время достаточно малыми (рис. 3.1, б).

Обозначим указанные отклонения через Axj, Джз, Джд. Тогда в динамическом процессе

§ 3.1]

ЛИНЕАРИЗАЦИЯ УРАВНБ1Й1Й

Это дифференциальное уравнение, так же как и (3.1), описывает тот же динамический процесс в том же звене автоматической системы. Отличие этого уравнения от прежнего состоит в следующем:

1) это уравнение является более приближенным, ибо в процессе его вьшода были отброшены малые высшего порядка;

2) неизвестными функциями времени в этом уравнении являются не-прежние полные величины х-, х, х, а их отклонения Ах, Ах, Дхз от некоторых установившихся значений х, ж ;

3) полученное уравнение является линейным относительно отклонений Дж1, Джг, Джа, Джд, . . ., Джд С постоянными коэффициентами j.

\ ёж ) неременными коэффициентами, если F содержит t в явном виде, а также когда установившийся процесс определяется неременнымк величинами х\ (г), х\ (г), % (О например в программном регулировании).

Таким образом,цель получения линейного дифференциального уравнения взамен преж- Рис. 3.2. него нелинейного достигнута.

Уравнение (3.5) называется дифференциальным уравнением звена в отклонениях. Проделав то же самое для всех звеньев системы, получим в результате линеаризованные уравнения процесса регулирования в отклонениях (или, как называют еще, уравнения в вариациях ).

В дальнейшем можно будет проводить линеаризацию нелинейных уравнений непосредственно но аналогии с формулой (3.5), не производя предварительных выкладок.

Приведем геометрическую трактовку этого способа линеаризации. Изобразим графически зависимость F от х- при постоянных значениях всех остальных неременных:

... а . *

Х = Ж2 = О, Жд = Xg, Жз = Жд = Жд = 0.

Пусть эта зависимость имеет вид кривой, представленной на рис. 3.2, а. Отметим значение ж и проведем в точке С касательную. Тогда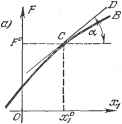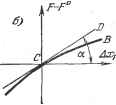

(3.6)

где а - угол наклона касательной в точке С (ж, F°), для которой

ж = ж

Замена ж = ж? + Дж и сокращение члена (3.7), производившиеся раньше аналитически, здесь эквивалентны переносу начала координат в точку С (рис. 3.2, а), в результате чего получается график рис. 3.2, б.

Первый член линейного уравнения (3.5) согласно (3.6) означает, что линеаризация уравнения геометрически может трактоваться как замена первоначальной кривой СВ на касательную к ней прямую CD. Из графика рис. 3.2, б очевидно, что эта замена тем точнее, чем меньшие величины отклонения Дж возникают в исследуемом динамическом процессе (основная предпосылка для линеаризации); границы отклонений Дж, для которых