ГЛАВА 15

ИМПУЛЬСНЫЕ СИСТЕМЫ

§ 15.1. Общие сведения

Линейной системой импульсного регулирования называется такая система автоматического регулирования, которая кроме звеньев, описываемых обыкновенными линейными дифференциальными уравнениями, содержит импульсное звено, преобразующее непрерывное входное воздействие в равноотстоящие друг от друга по времени импульсы.

В качестве импульсного звена (элемента) может использоваться падающая дужка гальванометра (рис. 1.28), генерирующая прямоугольные импульсы (рис. 15.1), у которых либо высота (рис. 15.1, а), либо ширина

TunI

ШХГ\

y=const а]

ТипИ

Рис. 15.1.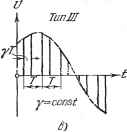

(рис. 15.1, пропорциональная непрерывной величине, поступающей на это звено в момент времени, совпадающий с началом импульса.

Кроме того, импульсным звеном может служить устройство типа ключа, которое (как и падающая дужка) по какой-то внешней причине производит замыкание цепи короткими импульсами через равные промежутки времени. Отличие импульсного звена типа ключа от импульсного звена типа падающей дужки состоит в тому что оно вырезает определенные участки из непрерывно изменяющегося воздействия (рис. 15.1, в). И те и другие импульсные звенья могут быть осуществлены различными электромеханическими или электронными устройствами. Будем называть их соответственно импульсными звенья ми типа I, типа II и типа III (рис. 15.1, а, б, в).

В качестве примера возьмем импульсную систему автоматического регу лирования температуры 0 (рис. 1.27). Структурная схема ее дана на рис. 15.2, а. Регулируемым объектом может являться, например, тепловой двигатель, температура в котором 0 должна поддерживаться постоянной путем изменения положения Е = ф шторок (регулирующего органа), т, е, путем Изменения интенсивности охлаждения двигателя.

В общем случае любая импульсная линейная система регулирования будет содержать ряд непрерывных звеньев, описываемых обыкновенньш?

линейными дифференциальными уравнениями, и хотя бы одно прерывное - импульсное звено. Поэтому можно изобразить обобщенную структурную схему импульсной системы регулирования так, как показано на рис. 15.2, б, где все непрерывные звенья сведены в один блок - непрерывную часть системы. Последняя меняет иметь какую угодно структуру (любой сложности, с обратными связями и т. п.). В данном примере в линейную часть входят: приводной двигатель, регулирующий орган (шторки), регулируемый объект и чувствительный элемент (термометр сопротивления с гальванометром).

В качестве импульсной системы можно также рассматривать системы регулирования с управляющими цифровыми вычислительными машинами

Непрерывная часть

Импульсное звено

Рис. 15.2.

(ЦВМ). Дискретный характер получения и обработки информации в ЦВМ приводит к так называемому квантованию по времени, что и позволяет применить здесь теорию импульсных систем. Однако системы с ЦВМ оказываются более сложными вследствие так называемого квантования по уровню, что делает их нелинейными. Поэтому теория импульсных систем в случае использования ЦВМ применима только для приближенных исследований, когда задача меняет быть линеаризована. Более подробно системы с ЦВМ будут рассмотрены в главе 24.

Импульсные фильтры. Ограничимся случаем, когда на выходе импульсного элемента импульсы отстоят друг от друга на одинаковые интервалы времени, продолжительность их такнсе одинакова и они отличаются друг от друга только по амплитуде (тип I и тип III на рис. 15.1).

Импульсная система может быть схематически представлена в виде соединения импульсного звена и непрерывной части. Последовательность импульсов на выходе импульсного

епрерь/Зная часть

Рис. 15.3.

звена после прохождения через непрерывную часть вследствие сглаживающих свойств последней превращается в непрерывные величины на выходе.

Обычно схема импульсной системы такова, что сигнал ошибки, полученный в элементе сравнения, поступает затем на импульсный элемент

(рис. 15.3). Импульсное звено на этой схеме изображено условно в виде ключа, который замыкается с периодом Т. Если время замыкания ключа мало по сравнению с периодом чередования Т и постоянными времени непрерывной части и если сигнал на входе ключа в течение времени, когда он замкнут, практически постоянен, то последовательность конечных по продолжительности импульсов на выходе ключа можно заменить последовательностью дельта-функций. Величина каждой дельта-функции (точнее, интеграла от нее по времени) будет пропорциональной значению сигнала на входе ключа в момент его замыкания.

ИМПУЛЬСНЫЕ СИСТЕМЫ

[гл; 15

%(Р)

Рис. 15.4.

Поскольку ключ замыкается в определенные моменты времени (О, Т, 2Т, ът и т. д.), то сигнал на входе необходимо рассматривать именно в эти моменты времени. Хотя на выходе непрерывной части сигнал и непрерывен, будем рассматривать его только в отдельные дискретные моменты времени.

Непрерывную часть совместно с ключом на ее входе будем называть импульсным фильтром (рис. 15.4). Более строго импульсный фильтр следует

определить как устройство, которое получает входные сигналы и одновременно дает выходные сигналы лишь в определенные моменты времени, например Г, 2Т, ЗГ и т. д. На входе непрерывной части с передаточной функцией Wo (р) действует дискретная функция X* [пТ], где п = О, ±1, ±2, ±3 и т. д. В соответствии со сказанным эта функция может быть представлена в виде последовательности дельта-функций.

На выходе будет непрерывная функция, определяемая в эти же дискретные моменты времени: у it) = у [пТ]., где п = О, ±1, ±2 и т. д.

Решетчатые функции. Введем понятие решетчатой функции времени / [пТ], или в сокращенной записи / [п], значения которой определены в дискретные моменты времени t = пТ, где п - целое число, а Т - период повторения. Операция замены непрерывной функции решетчатой

f[n]=f (t) I (15.1)

показана на рис. 15.5. Изображенные на рис. 15.5, б ордашаты представляют собой так называемые дискреты исходной непрерывной функции / (t) при t = пТ (рис. 15.5, а).

Дискреты / {t) могут быть также определены для смещенных моментов времени t = пТ АТ = in + е) т. Смещение АТ - const может быть положительной или отрицательной величиной при выполнении условия \ АТ \<С Т. Относитель-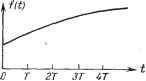

ZT 37 4т

, ПпТ,АТ]

Т ZT ЗТ 4Т Рис. 15.5.

ное смещение & = АТ-Т~ по модулю меньше единицы. ф

Образование смеиенной решетчатой функции f{nT, ДГ], или в сокращенной J i ---пТ

записи / [п, si, из непрерывной функции / {t) для случ4я ДГ >- О изображено на рис. 15.5, в.

В последующем изложении будем считать, что в решетчатой функции / [п, s] аргумент п О и параметр s >- 0. В случае необходимости рассмотрения функции / Ы, Sq] с отрицательным параметром во < О дискретное время можно представить в виде [(п - 1) -j- (1 -f- So)] Г = [(n - 1) + е] Т. Тогда решетчатая функция может быть записана в виде f [п - 1, s], где е = 1 + So.

Решетчатая функция не обязательно должна формироваться из некоторой исходной непрерывной. Любая числовая последовательность некоторой величины, определенная в дискретные равноотстояпще моменты времени, может быть представлена в виде решетчатой функции.

Заметим, что обратная задача - формирование непрерывной функции из решетчатой - не может быть решена однозначно, так как функции, задан-