или, с учетом (14.25), (14.27) и (14.37)

Сравнивая (14.61) и (14.62), получаем искомое уравнение регулируемого объекта (трубопровода) без учега волповых процессов:

Гоф + Рф = I, (14.63)

= P = f() . (14.64)

Исключив отсюда переменные и г], приходим к одному дифференциальному уравнению данной системы автоматического регулирования:

{(Г?р2 + Г2Р +1) {TsP +1) [(1 + Ъе-) +1 (1 - Ъе-)\ + (1 + Ье--)} Ф = О,

которое преобразуется к виду

{ [{Т1р -Ь ТР +1) {Tsp +1) -Ь -h

[(Г?Р+Г2Р + 1) {Т,р+\) + у-] Ф = 0. (14.59)

Это уравнение имеет в основном тот же вид, что и уравнение системы с запаздыванием (например, (14 19) и (14.20)). Здесь оно определяет величину Ф, через которую затем находятся из вьппенаписанных соотношений регулируемая величина и другие. Параметр т в этом уравнении согласно (14.54) и (14.30) вьшисляется по формуле

т==2 4-, (14.60)

т. е. г есть удвоенное время прохождения звука в газе по данному трубопроводу.

Уравнение системы регулирования без учета волновых процессов. Интересно сравнить полученное дифференциально-разностное уравнение (14.59) с тем, которое получилось бы, если не учитьгеать волновых явлений в трубопроводе. Будем считать, что весь газ в трубопроводе движется, как единая масса с единой скоростью и давлением, при этом учтем, конечно, сжимаемость газа.

Будем считать, что приток и потребление газа в единицу времени в этом случае будут = (х), G = G {р). Изменение количества газа, находящегося в трубопроводе, в единицу времени будет - G,; но

Gi - = (Gj-G ) - (G - GO) = AGi - ДС2 - () Д :г - () Др-используя (14.35), (14.36) и (14.27), получим

с другой стороны, количество газа (по весу) равно gpFL, так как FL есть объем трубопровода. Поэтому изменение количества газа в единицу времени,

используя (14.24) и соотношение i, запишем в виде

Следовательно, в этом случае вместо дифференциального уравнения третьего порядка с запаздываюхцим аргументом (14.59) получается обыкновенное дифференциальное уравнение четвертого порядка.

§ 14.3. Исследование устойчивости и качества регулирования

В § 14.1 были приведены уравнения линейных систем с запаздыванием, которые для разомкнутой цепи имели вид

Q(p)xz = R(l>) e-vx, (14.67)

а для замкнутой системы

D{p)x = N{p) /, (14.68)

D{p) = Qip) + R{p)e--p, iV(p) = -M. (14.69)

В § 14.2 при выводе уравнений для одной линейной системы автоматического регулирования с распределенными параметрами было показано, что они сводятся к тому же самому виду во всех тех случаях, когда распределенное звено системы описывается волновьш уравнением в частных производных типа (14.31) или (14.29).

Характеристическое уравнение для таких систем с распределенньши параметрами и систем с запаздыванием имеет согласно (14.69) трансцендентный вид

Q{p) + R (Р) е-Р = О, (14.70)

где Q (р) ж R (р) - обыкновенные многочлены, причем степень R (р) обычно меньше или в крайнем случае равна степени Q (р).

Уравнение (14.70) записывается иногда и в другом виде, например:

Q (р) е-Р + R (р) е-р = О

Q (р) сЪтр + R {р) sh тр = 0.

Могут встретиться уравнения и более сложного вида:

Q (Р) + Ri (Р) е-Р + R, (р) е-Р = О, Q (р) ёР -Ь i?i {р) е-р + Rz (р) = О

и т. п.

Здесь Tq - прежняя постоянная объекта (14.30), а Р - новый постоянный параметр объекта, в выражении которого значение частной производной определяется для заданного объекта графически, аналогично рис. 14.8, или же расчетным путем.

К этому же уравнению объекта присоединяются прежние уравнения регулятора (14.47) - (14.51), где заменяется на ф. Следовательно, в символической операторной форме уравнения данной системы регулирования давления без учета волновых явлений будут:

{Т\р + TzP+i) 1] = -/Ф, [ (14.65) (Г.р+1) = г] J

ЦТоР + Р) {Т1р + TzP + 1) {TsP + 1) + A;J ф = 0. (14.66)

Рассмотрим характеристическое уравнение вида (14.70). Известно, что решение дифференциально-разностных уравнений (14.68) можно записать в виде некоторых рядов и что для затухания этого решения, т. е. для устойчивости системы, необходимо и достаточно, чтобы все корни трансцендентного характеристического уравнения (14.70) имели отрицательные вещественные части. Но в отличие от обыкновенного алгебраического уравнения здесь вследствие наличия множителя е-Р уравнение может иметь бесконечное количество корней.

К указанным системам применимы критерий устойчивости Михайлова и критерий устойчивости Найквиста в их прежних формулировках (см. гла-, ву 6). Однако здесь вследствие

а X

наличия множителя е~ сущест венно изменяется очертание как кривой Михайлова замкнутой системы

D Осо) = Q (ja) + R (/(о) е- ,

(14.71)

так и амплитудно-фазовой характеристики разомкнутой цепи, построенной по частотной передаточной функции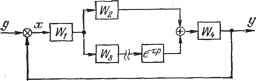

Рис. 14.9.

причем размыкание системы производится по определенному правилу, которое дается ниже.

Из кривой Михайлова не получается таких простых алгебраических выражений, как в § 6.3. Как следствие, для устойчивости линейных систем первого и второго порядка с запаздыванием, оказывается, уже недостаточно только положительности коэффициентов, а для систем третьего и более высокого порядка с запаздыванием неприменимы критерии устойчивости Вышнеградского, Рауса и Гурвица.

Ниже будет рассмотрено определение устойчивости только по критерию Найквиста, так как его использование для этой цели оказывается наиболее простым.

Построение амплитудно-фазовой характеристики и исследование устойчивости по критерию Найквиста луяше всего производить, если передаточная функция разомкнутой системы представлена в виде (14.72). Для получения этого необходимо произвести соответствующим образом размыкание системы.

Для случая, изображенного на рис. 14.9, а, размыкание можно сделать в любом месте главной цепи, например так, как это показано. Тогда передаточная функция разомкнутой системы будет

что совпадает по форме с (14.72).