D (р) = (Tlp + Т,р + 1){р + kgk,k,) р + Kkkjte-v, . (14.20)

N{p) = ~{гу + + 1) (р + kgkji,). ]

Здесь Дсо, Ау, Ах, Ах* - приращения скорости, перемещений золотника и регулирующего органа и управляющего воздействия; fcj, . . ., 5 - коэффициенты, 2 и Г4 - постоянные времени.

§ 14.2. Уравнения линейных систем с распределенными параметрами

Системой автоматического регулирования с распределенными параметрами называется такая система, среди уравнений которой кроме обыкновенных дифференциальных уравнений имеются уравнения в частных производных. Физически это соответствует учету волновых явлений или гидравлического удара в трубопроводах, учету волновых процессов в длинных электрических линиях при передаче по ним воздействий от одного звена системы автоматического регулирования к другому или же при регулировании процессов в самих трубопроводах или длинных линиях.

Этот вопрос приобретает практическое значение чаще всего в некоторых системах регулирования, включающих в себя водяные, масляные или газовые трубопроводы (либо в объекте, либо в регуляторе), реже - в некоторых системах телерегулирования (телеуправления) и т. п.

Известно, например, что водяной трубопровод гидротурбины описывается без учета потерь уравнениями

8v 8h 8h а? dv

dt дх dt g dx

где V - скорость движения воды, h - напор в произвольной точке, определяемой координатой X вдоль трубопровода, а - скорость звука в воде. Уравнения длинной электрической линии без потерь имеют вид

du jdi di du

дх dt \ dx 8t

где и - напряжение, i - ток в произвольной точке, определяемой координатой X вдоль линии, I и с - индуктивность и емкость единицы длины линии.

После решения указанных уравнений в частных производных с учетом, граничных условий, определяемых смежными звеньями данной системы автоматического регулирования, для системы в целом получаются дифференциально-разностные уравнения того же типа, как и для систем с запаздыванием (§ 14.1).

И снабжен регулятором с жесткой обратной связью (рис. 10.11). Уравнения такой системы

pA(u = kiAx*~f{t), {Tlp + T,p+i)Ay=k,A<

{р + hjijib) Ах=- kski Ау, Ах* = е-Р Ах.

Уравнение замкнутой системы

D (р) А(о = N (р) f (t), (14.19)

Рассмотрим вывод уравнений системы автоматического регулирования давления газа в трубопроводе, схема которой изображена на рис. 14.7. В данном случае сам регулируемый объект (трубопровод) является звеном с распределенными параметрами. Для простоты будем считать его ,?, jj, прямолинейным, а всех потре- бителей - сосредоточенными на конце трубопровода.

Регулятор состоит из чувствительного элемента 2 (мембранный измеритель давления), усилителей 3 ш 4 (струйная трубка и пневматический двигатель) с жесткой обратной связью 5 и из регулирующего органа 6 (клапан). Возмущающее воздействие / (t) на объект выражается в изменении по произволу потребителей некоторого эквивалентного выходного сечения на конце трубопровода.

Уравнение регулируемого объекта. Движение газа в трубопроводе подчиняется уравнению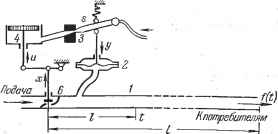

Рис. 14.7.

dw dw 1

Учтем также условие постоянства массы

+ -- = 0

и адиабатическое уравнение состояния газа

(14.21)

(14.22)

(14.23)

В этих уравнениях w, р, р -- соответственно скорость, давление и плотность газа в текущем сечении трубопровода с координатой I в момент времени t (вся длина трубопровода обозначается через L); к - показатель степени в уравнении адиабатического состояния газа; индексы О вверху (р°, р ) означают, что данные величины относятся к установившемуся состоянию системы. Продифференцировав (14,23), получаем

k l±-Y 1 ф 1 др;

откуда

ро dt рО dt

dp 1 / рО \Ь-1 др dt \ р ) dt

где а - скорость звука в газе, определяемая формулой

Р ь

(14.24)

(14.25)

Обычно не учитывают сопротивления движения газа в трубопроводе, пренебрегая сравнительно малыми членами и- и Кроме того, ввиду

малости величины отклонения давления р в процессе регулирования от его

установившегося значения можно считать, что

1, а следовательно.

согласно (14.23)

1. Б результате из уравнений (14.21), (14.22) и (14.24)

y>dt~ д% <> dt- (-

где введены два постоянных параметра регули-1 6 j-gMO руемого объекта:

г r. = i, v = J?. (14.30)

jL-Первый из них (Tq) представляет собой, очевидно.

Рис. 14.8.

время прохождения газа по данному трубопроводу в установившемся процессе, а второй (у) - отношение установившейся скорости газа к скорости звука в нем.

Заметим, что уравнения (14.29) эквивалентны так называемому волновому уравнению

(1-31)

которое легко получается, если первое из уравнений (14.29) продифференцировать по К, а второе - по г и сравнить результаты дифференцирования.

Для системы уравнения в частных производных (14.29) надо написать граничные условия. Для этого запишем уравнение поступления газа через регулирующий клапан в начале трубопровода и уравнение потребления газа в конце его.

Используем выражение для скорости газа через его расход, а именно

(14.32)\

gpF

где G - расход газа по весу в секунду, F - площадь сечения трубопровода, g - ускорение силы тяжести.

Условимся значения всех переменных, относящихся к началу и к концу трубопровода, обозначать индексами 1 и 2 соответственно. Расход газа в начале трубопровода G будем считать функцией координаты перемещения регулирующего клапана х, т. е.

Gi = Gi ()- (14.33)

Эта функция (рис. 14.8) определяется либо аналитическим расчетом, либо (ИЗ опытных данных.

получаем

dt ро dl 61 ,р0а2 et Ц.о;

Введем обозначения для относительного отклонения ф регулируемой Величины от ее установившегося значения и для относительной координаты К вдоль трубопровода:

= = 4- (0<<1). (14.27)

а также для относительного отклонения ф скорости движения газа в трубопроводе:

где - скорость газа в трубопроводе при установившемся процессе, к - показатель степени в адиабатическом уравнении состояния газа (14.23).

Переходя в уравнениях (14.26) к этим относительным безразмерным переменным и бесконечно малым прирап1;ениям, получаем искомые уравнения

регулируемого объекта (трубопровода) в виде